题目内容
14．
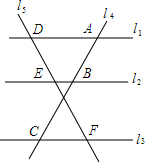如图，已知直线l1、l2、l3分别截直线l4于点A、B、C，截直线l5于点D、E、F，且l1∥l2∥l3．（1）如果AB=4，BC=8，EF=12，求DE的长．
（2）如果DE：EF=2：3，AB=6，求AC的长．
分析 （1）由平行线分线段成比例定理得出比例式，即可得出DE的长；
（2）由平行线分线段成比例定理得出比例式，求出BC的长，即可得出AC的长．
解答 解：（1）∵l1∥l2∥l3．
∴$\frac{DE}{EF}=\frac{AB}{BC}$=$\frac{4}{8}$=$\frac{1}{2}$，
∴DE=$\frac{1}{2}$EF=6；
（2）∵l1∥l2∥l3．
∴$\frac{DE}{EF}=\frac{AB}{BC}$=$\frac{2}{3}$，
∴BC=$\frac{3}{2}$AB=$\frac{3}{2}$×6=9，
∴AC=AB+BC=6+9=15．
点评 本题考查了平行线分线段成比例定理；熟练掌握平行线分线段成比例定理，并能进行推理计算是解决问题的关键．
练习册系列答案
相关题目
4．将方程x2-x-1=0的左边变成完全平方式后，方程是（ ）
| A． | ${（x+\frac{1}{2}）^2}=\frac{5}{4}$ | B． | ${（x-\frac{1}{2}）^2}=\frac{5}{4}$ | C． | ${（x-\frac{1}{2}）^2}=\frac{3}{2}$ | D． | ${（x+\frac{1}{2}）^2}=\frac{3}{2}$ |
已知线段PQ，在PQ上求作一点D，使PD：DQ=2：1．