题目内容
4.已知$\frac{1}{2}×\frac{2}{3}=\frac{1}{3},\frac{1}{2}×\frac{2}{3}×\frac{3}{4}=\frac{1}{4},\frac{1}{2}×\frac{2}{3}×\frac{3}{4}×\frac{4}{5}=\frac{1}{5}$,…,$\frac{1}{2}×\frac{2}{3}×\frac{3}{4}×…×\frac{n}{n+1}=\frac{1}{n+1}$,根据规律求:$(\frac{1}{2}-1)$×$(\frac{1}{3}-1)×(\frac{1}{4}-1)×…×(\frac{1}{100}-1)$.
分析 首先判定符号,有100-2+1=99个负因数,计算结果为负,再进一步利用约分的规律交错约分得出答案即可.
解答 解:原式=-$\frac{1}{2}$×$\frac{2}{3}$×$\frac{3}{4}$×$\frac{4}{5}$×…×$\frac{99}{100}$
=-$\frac{1}{100}$.
点评 此题考查有理数的混合运算,掌握运算的方法与符号的判定是解决问题的关键.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
13.设n是正整数,则10n+1是( )
| A. | n个10相乘所得的积 | B. | 一个(n+1)位的整数 | ||
| C. | 10后面有(n+1)个0的整数 | D. | 一个(n+2)位的整数 |
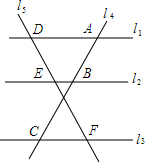 如图,已知直线l1、l2、l3分别截直线l4于点A、B、C,截直线l5于点D、E、F,且l1∥l2∥l3.
如图,已知直线l1、l2、l3分别截直线l4于点A、B、C,截直线l5于点D、E、F,且l1∥l2∥l3. 如图,在一圆柱的下底边沿A处有一只蚂蚁,它不走直线而是绕着圆柱侧面,找出蚂蚁到B处的最短路径.
如图,在一圆柱的下底边沿A处有一只蚂蚁,它不走直线而是绕着圆柱侧面,找出蚂蚁到B处的最短路径.
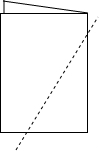 把一张长方形纸对折,任意剪出一个直角边在折线上的直角三角形,把它展开,得到三角形记为△ABC,并将折线的另一端点记为D,如图所示,这是什么特殊三角形?图中有哪些相等的角?有哪些相等的线段?在△ABC中,AD有几种角色?各是什么?
把一张长方形纸对折,任意剪出一个直角边在折线上的直角三角形,把它展开,得到三角形记为△ABC,并将折线的另一端点记为D,如图所示,这是什么特殊三角形?图中有哪些相等的角?有哪些相等的线段?在△ABC中,AD有几种角色?各是什么?