题目内容
12.如图,每个图案都由若干个“●”组成,其中第①个图案中有7个“●”,第②个图案中有13个“●”,…,则第⑨个图案中“●”的个数为( )
| A. | 57 | B. | 73 | C. | 91 | D. | 111 |
分析 根据第①个图案中“●”有:1+3×(0+2)个,第②个图案中“●”有:1+4×(1+2)个,第③个图案中“●”有:1+5×(2+2)个,第④个图案中“●”有:1+6×(3+2)个,据此可得第⑨个图案中“●”的个数.
解答 解:∵第①个图案中“●”有:1+3×(0+2)=7个,
第②个图案中“●”有:1+4×(1+2)=13个,
第③个图案中“●”有:1+5×(2+2)=21个,
第④个图案中“●”有:1+6×(3+2)=31个,
…
∴第9个图案中“●”有:1+11×(8+2)=111个,
故选:D.
点评 本题考查规律型:图形的变化,解题的关键是将原图形中的点进行无重叠的划分来计数.

练习册系列答案
相关题目
2.等腰直角三角形三边长度之比为( )
| A. | 1:1:2 | B. | 1:1:$\sqrt{2}$ | C. | 1:2:$\sqrt{3}$ | D. | 不能确定 |
7.下列各数中,最小的数是( )
| A. | 0 | B. | -1 | C. | -$\sqrt{2}$ | D. | -2 |
17.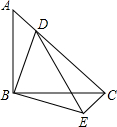 如图,等腰Rt△ABC中,BA=BC,∠ABC=90°,点D在AC上,将△ABD绕点B沿顺时针方向旋转90°后,得到△CBE.
如图,等腰Rt△ABC中,BA=BC,∠ABC=90°,点D在AC上,将△ABD绕点B沿顺时针方向旋转90°后,得到△CBE.
(1)求∠DCE的度数;
(2)若AB=4,CD=3AD,求DE的长.
 如图,等腰Rt△ABC中,BA=BC,∠ABC=90°,点D在AC上,将△ABD绕点B沿顺时针方向旋转90°后,得到△CBE.
如图,等腰Rt△ABC中,BA=BC,∠ABC=90°,点D在AC上,将△ABD绕点B沿顺时针方向旋转90°后,得到△CBE.(1)求∠DCE的度数;
(2)若AB=4,CD=3AD,求DE的长.
1. O为△ABC外心,∠BOC=40°,则∠BAC=( )
O为△ABC外心,∠BOC=40°,则∠BAC=( )
 O为△ABC外心,∠BOC=40°,则∠BAC=( )
O为△ABC外心,∠BOC=40°,则∠BAC=( )| A. | 40° | B. | 30° | C. | 20° | D. | 10° |
2. 如图,△A1B1A2,△A2B2A3,△A3B3A4,…△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上,已知OA2=1,则OA2016的长为( )
如图,△A1B1A2,△A2B2A3,△A3B3A4,…△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上,已知OA2=1,则OA2016的长为( )
 如图,△A1B1A2,△A2B2A3,△A3B3A4,…△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上,已知OA2=1,则OA2016的长为( )
如图,△A1B1A2,△A2B2A3,△A3B3A4,…△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上,已知OA2=1,则OA2016的长为( )| A. | 22013 | B. | 22014 | C. | 22015 | D. | 22016 |
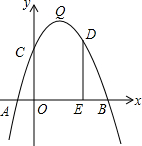 如图,抛物线y=-x2+bx+c的顶点为Q,抛物线与x轴交于A(-1,0),B(5,0)两点,与y轴交于点C.
如图,抛物线y=-x2+bx+c的顶点为Q,抛物线与x轴交于A(-1,0),B(5,0)两点,与y轴交于点C. 如图,矩形ABCD的边AB=3,AD=4,点E从点A出发,沿射线AD移动,以CE为直径作圆O,点F为圆O与射线BD的公共点,连结EF、CF,过点E作EG⊥EF,EG与圆O相交于点G,连结CG.
如图,矩形ABCD的边AB=3,AD=4,点E从点A出发,沿射线AD移动,以CE为直径作圆O,点F为圆O与射线BD的公共点,连结EF、CF,过点E作EG⊥EF,EG与圆O相交于点G,连结CG.