题目内容
14. 如图,在△ABC中,DE∥BC,DE分别交AB,AC于点D,E,若AD:DB=1:2,则△ADE与△ABC的面积之比是( )
如图,在△ABC中,DE∥BC,DE分别交AB,AC于点D,E,若AD:DB=1:2,则△ADE与△ABC的面积之比是( )| A. | 1:3 | B. | 1:4 | C. | 1:9 | D. | 1:16 |
分析 根据DE∥BC,即可证得△ADE∽△ABC,然后根据相似三角形的面积的比等于相似比的平方,即可求解.
解答 解:∵AD:DB=1:2,
∴AD:AB=1:3,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{1}{3}$)2=$\frac{1}{9}$.
故选:C.
点评 本题考查了三角形的判定和性质:熟练掌握相似三角形的面积比是相似比的平方是解题的关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
4.若|x|=2,y2=9,且xy<0,则x-y等于( )
| A. | 1或-1 | B. | 5或-5 | C. | 1或5 | D. | -1或-5 |
9.已知点A、B、C在同一条直线上,线段AC=3cm,线段BC=2cm,则线段AB的长为( )cm.
| A. | 1 | B. | 5 | C. | 1 或5 | D. | 6 |
6.计算-2×3结果正确的是( )
| A. | 6 | B. | -6 | C. | 5 | D. | -5 |
3. 如图,AB=AD,要说明△ABC≌△ADE,需添加的条件不能是( )
如图,AB=AD,要说明△ABC≌△ADE,需添加的条件不能是( )
 如图,AB=AD,要说明△ABC≌△ADE,需添加的条件不能是( )
如图,AB=AD,要说明△ABC≌△ADE,需添加的条件不能是( )| A. | ∠E=∠C | B. | AC=AE | C. | ∠ADE=∠ABC | D. | DE=BC |
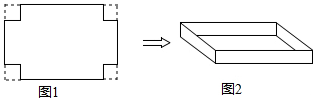 一张长为30cm,宽20cm的矩形纸片,如图1所示,将这张纸片的四个角各剪去一个边长相同的正方形后,把剩余部分折成一个无盖的长方体纸盒,如图1所示,如果折成的长方体纸盒的底面积为264cm2,求剪掉的正方形纸片的边长.
一张长为30cm,宽20cm的矩形纸片,如图1所示,将这张纸片的四个角各剪去一个边长相同的正方形后,把剩余部分折成一个无盖的长方体纸盒,如图1所示,如果折成的长方体纸盒的底面积为264cm2,求剪掉的正方形纸片的边长.