题目内容
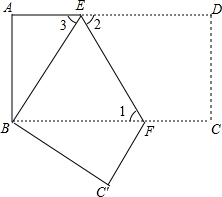 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.(1)折叠后,DC的对应线段是
(2)若∠1=50°,求∠2,∠3的度数;
(3)若AB=7,DE=8,求CF的长度.
考点:翻折变换(折叠问题)
专题:
分析:(1)由翻折的性质直接得出答案即可;
(2)由AD∥BC得∠1=∠2,所以∠2=∠BEF=50°,从而得∠3=180-∠2-∠BEF;
(3)首先根据角角之间的关系得到BE=BF,结合∠A=∠C′,AB=BC′,证明出△ABE≌△C′BF,进一步得到AE=FC,在Rt△ABE中,利用AB2+AE2=BE2,求出AE的长,进而求出CF的长.
(2)由AD∥BC得∠1=∠2,所以∠2=∠BEF=50°,从而得∠3=180-∠2-∠BEF;
(3)首先根据角角之间的关系得到BE=BF,结合∠A=∠C′,AB=BC′,证明出△ABE≌△C′BF,进一步得到AE=FC,在Rt△ABE中,利用AB2+AE2=BE2,求出AE的长,进而求出CF的长.
解答:解:(1)折叠后,DC的对应线段是BE,CF的对应线段是C′F;
(2)∵AD∥BC,
∴∠1=∠2=50°.
∵∠BEF=∠2=50°,
∴∠3=180-∠2-∠BEF=80°;
(3)∵∠1=∠2,∠BEF=∠2,
∴∠1=∠BEF,
∴BE=BF.
又∵∠A=∠C′,AB=BC′,
∵
,
∴△ABE≌△C′BF(SAS),
∴AE=C′F.
∵FC=FC′,
∴AE=FC.
在Rt△ABE中,AB2+AE2=BE2.
∵AB=7,BE=DE=8,
∴AE=
,
∴CF=AE=
.
(2)∵AD∥BC,
∴∠1=∠2=50°.
∵∠BEF=∠2=50°,
∴∠3=180-∠2-∠BEF=80°;
(3)∵∠1=∠2,∠BEF=∠2,
∴∠1=∠BEF,
∴BE=BF.
又∵∠A=∠C′,AB=BC′,
∵
|
∴△ABE≌△C′BF(SAS),
∴AE=C′F.
∵FC=FC′,
∴AE=FC.
在Rt△ABE中,AB2+AE2=BE2.
∵AB=7,BE=DE=8,
∴AE=
| 15 |
∴CF=AE=
| 15 |
点评:此题考查图形的翻折变换,解题过程中应注意折叠前后的对应关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
△ABC的外心为O,∠BOC=60°,则∠BAC=( )
| A、30° |
| B、60° |
| C、30°或150° |
| D、60°或120° |
 小明同学从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:
小明同学从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息: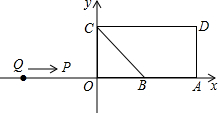 如图,A(10,0),B(6,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°,点P从点Q(-8,0)出发,沿x轴向右以每秒2个单位的速度运动,运动时间为t秒.
如图,A(10,0),B(6,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°,点P从点Q(-8,0)出发,沿x轴向右以每秒2个单位的速度运动,运动时间为t秒. 如图,△ABC中,AD平分∠BAC,点E、F分别在AB、AC边上,且AE=AF,求证:∠BED=∠DFC.
如图,△ABC中,AD平分∠BAC,点E、F分别在AB、AC边上,且AE=AF,求证:∠BED=∠DFC.