题目内容
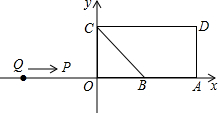 如图,A(10,0),B(6,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°,点P从点Q(-8,0)出发,沿x轴向右以每秒2个单位的速度运动,运动时间为t秒.
如图,A(10,0),B(6,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°,点P从点Q(-8,0)出发,沿x轴向右以每秒2个单位的速度运动,运动时间为t秒.(1)求点C的坐标;
(2)当∠BCP=15°时,求t的值;
(3)以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在直线)相切时,求t的值.
考点:圆的综合题
专题:
分析:(1)由A,B的坐标及∠CBO=45°可得出点C的坐标为(0,6);
(2)分为两种情况:①当P在点B的左侧时,②当P在点B的右侧时,分别求出t的值,
(3)本小题分三种情况讨论:①当PC⊥BC时,⊙P与BC相切;②当PC⊥CD时,⊙P与CD相切;③当PA⊥AD时,⊙P与AD相切;分别求出各种情况的t的值.
(2)分为两种情况:①当P在点B的左侧时,②当P在点B的右侧时,分别求出t的值,
(3)本小题分三种情况讨论:①当PC⊥BC时,⊙P与BC相切;②当PC⊥CD时,⊙P与CD相切;③当PA⊥AD时,⊙P与AD相切;分别求出各种情况的t的值.
解答:解:(1)∵A(10,0),B(6,0),
∴OA=10,OB=6,
∵∠CBO=45°,
∴OC=OB=6,
∴点C的坐标(0,6);
(2)①当P在点B的左侧时,
∵∠CBO=45°,∠BCP=15°
∴∠OCP=∠OCB-∠BCP=45°-15°=30°,
∵CO=6,
∴OP=
CO=2
,
∵Q(-8,0),
∴QP=2
+8,
∵点P沿x轴向右以每秒2个单位的速度运动,
∴t=
+4,
②当P在点B的右侧时,
∵∠CBO=45°,∠BCP=15°
∴∠OCP=∠OCB+∠BCP=45°+15°=60°,
∵CO=6,
∴OP=
CO=6
,
∵Q(-8,0),
∴QP=6
+8,
∵点P沿x轴向右以每秒2个单位的速度运动,
∴t=3
+4,
综上所述当∠BCP=15°时,t的值为
+4或3
+4.
(3)①如图1,当PC⊥BC时,⊙P与BC相切,
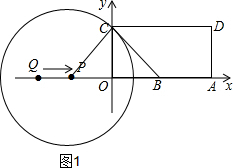
∵∠CBO=45°,
∴∠CPB=45°,CP=BC,
∵CO=6,
∴PO=6,
∴QP=QO-PO=8-6=2,
∵点P从点Q(-8,0)出发,沿x轴向右以每秒2个单位的速度运动,
∴t=1(秒),
②如图2,当PC⊥CD时,⊙P与CD相切,
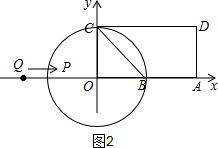
∵QO=8,点P从点Q(-8,0)出发,沿x轴向右以每秒2个单位的速度运动,
∴t=8÷2=4(秒)
③如图3,当PA⊥AD时,⊙P与AD相切,设PA=r
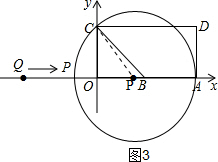
∵OA=10,OC=6,
∴OP2+OC2=PC2,即(10-r)2+62=r2,解得r=
,
∴QP=8+10-
=
,
∵点P从点Q(-8,0)出发,沿x轴向右以每秒2个单位的速度运动,
∴t=
,
综上所述t1=1秒,t2=4秒,t3=
秒.
∴OA=10,OB=6,
∵∠CBO=45°,
∴OC=OB=6,
∴点C的坐标(0,6);
(2)①当P在点B的左侧时,
∵∠CBO=45°,∠BCP=15°
∴∠OCP=∠OCB-∠BCP=45°-15°=30°,
∵CO=6,
∴OP=
| ||
| 3 |
| 3 |
∵Q(-8,0),
∴QP=2
| 3 |
∵点P沿x轴向右以每秒2个单位的速度运动,
∴t=
| 3 |
②当P在点B的右侧时,
∵∠CBO=45°,∠BCP=15°
∴∠OCP=∠OCB+∠BCP=45°+15°=60°,
∵CO=6,
∴OP=
| 3 |
| 3 |
∵Q(-8,0),
∴QP=6
| 3 |
∵点P沿x轴向右以每秒2个单位的速度运动,
∴t=3
| 3 |
综上所述当∠BCP=15°时,t的值为
| 3 |
| 3 |
(3)①如图1,当PC⊥BC时,⊙P与BC相切,

∵∠CBO=45°,
∴∠CPB=45°,CP=BC,
∵CO=6,
∴PO=6,
∴QP=QO-PO=8-6=2,
∵点P从点Q(-8,0)出发,沿x轴向右以每秒2个单位的速度运动,
∴t=1(秒),
②如图2,当PC⊥CD时,⊙P与CD相切,

∵QO=8,点P从点Q(-8,0)出发,沿x轴向右以每秒2个单位的速度运动,
∴t=8÷2=4(秒)
③如图3,当PA⊥AD时,⊙P与AD相切,设PA=r

∵OA=10,OC=6,
∴OP2+OC2=PC2,即(10-r)2+62=r2,解得r=
| 34 |
| 5 |
∴QP=8+10-
| 34 |
| 5 |
| 56 |
| 5 |
∵点P从点Q(-8,0)出发,沿x轴向右以每秒2个单位的速度运动,
∴t=
| 28 |
| 5 |
综上所述t1=1秒,t2=4秒,t3=
| 28 |
| 5 |
点评:本题主要考查了圆的综合题,解题的关键是分类讨论当⊙P与四边形ABCD的边(或边所在直线)相切的三种情况.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
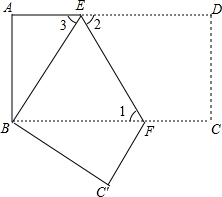 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.