题目内容
如图，△ABC中，AD平分∠BAC，点E、F分别在AB、AC边上，且AE=AF，求证：∠BED=∠DFC．考点：全等三角形的判定与性质
专题：证明题
分析：求出∠EAD=∠FAD，根据SAS推出△EAD≌△FAD，根据全等三角形的性质得出∠AED=∠AFD，即可得出答案．
解答：证明：∵AD平分∠BAC，
∴∠EAD=∠FAD，
在△EAD和△FAD中
∴△EAD≌△FAD（SAS），
∴∠AED=∠AFD，
∵∠BED+∠AED=180°，∠AFD+∠DFC=180°，
∴∠BED=∠DFC．
∴∠EAD=∠FAD，
在△EAD和△FAD中
|
∴△EAD≌△FAD（SAS），
∴∠AED=∠AFD，
∵∠BED+∠AED=180°，∠AFD+∠DFC=180°，
∴∠BED=∠DFC．
点评：本题考查了全等三角形的性质和判定的应用，注意：全等是三角形的对应边相等，对应角相等．
练习册系列答案
相关题目
由四舍五入法得到的近似数6.50×104是精确到（ ）
| A、百分位 | B、百位 | C、十位 | D、个位 |
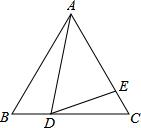已知边长为9的正三角形ABC中，BD=3，∠ADE=60°，则AD=
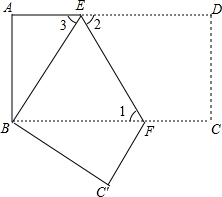如图，把长方形纸片ABCD沿EF折叠后，使得点D与点B重合，点C落在点C′的位置上．
如图，已知∠A=∠B=90°，AB=7、AD=2、BC=3，P在AB上，且△PAD∽△PBC，求AP的长．
如图，从塔吊的顶部A处与其横臂上B、C两处扯两条钢丝线，已知AD长为4m，后臂BD长为3m，BC长10.5m，求两条拉线长度各为多少？