题目内容
△ABC的外心为O，∠BOC=60°，则∠BAC=（ ）
| A、30° |
| B、60° |
| C、30°或150° |
| D、60°或120° |
考点：三角形的外接圆与外心
专题：
分析：根据题意画出图形，按点A在优弧
上或在劣弧
上两种情况分类讨论，问题即可解决．
 |
| BC |
|
| BC |
解答：
解：如图，
当点A在优弧
上时，
∵∠BOC=60°，
∴∠A=30°；
当点A在劣弧
上时，
∠A=180°-30°=150°，
故选：C．
解：如图，当点A在优弧
|
| BC |
∵∠BOC=60°，
∴∠A=30°；
当点A在劣弧
|
| BC |
∠A=180°-30°=150°，
故选：C．
点评：该题以三角形的外接圆为载体，主要考查了圆周角定理及其推论的应用问题；根据题意做出符合题意的几何图形是解题的关键．
练习册系列答案
相关题目
已知，△ABC≌△DEF，且∠A=55°，∠E=45°，则∠C=（ ）
| A、55° | B、45° |
| C、80° | D、90° |
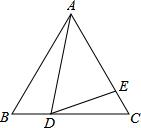已知边长为9的正三角形ABC中，BD=3，∠ADE=60°，则AD=
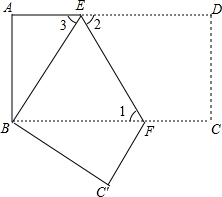如图，把长方形纸片ABCD沿EF折叠后，使得点D与点B重合，点C落在点C′的位置上．