题目内容
4.分解因式:(1)2a3-4a2b+2ab2=2a(a-b)2
(2)4x2+3(4xy+3y2)=(2x+3y)2.
分析 (1)根据提公因式,可得完全平方公式,再根据完全平方公式,可得答案;
(2)根据完全平方公式,可得答案.
解答 解:(1)2a3-4a2b+2ab2=2a(a2-2ab+b2)=2a(a-b)2;
(2)4x2+3(4xy+3y2)=4x2+12xy+9y2=(2x+3y)2.
故答案为:2a(a-b)2,(2x+3y)2.
点评 本题考查了因式分解,利用提公因式、完全平方公式是解题关键,注意分解要彻底.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
14.下面计算正确的是( )
| A. | -0.25ab+$\frac{1}{4}$ab=0 | B. | 3a2+2a3=5a5 | C. | 3+x=3x | D. | 3x2-x2=3 |
15. 如图,二次函数y=-$\frac{5}{8}$x2+$\frac{7}{4}$x+3的图象与x轴交于点A、B,与y轴交于点C,点D在该抛物线上,且点D的横坐标为2,连接BC、BD,设∠OCB=α,∠DBC=β,则cos(α-β)的值是( )
如图,二次函数y=-$\frac{5}{8}$x2+$\frac{7}{4}$x+3的图象与x轴交于点A、B,与y轴交于点C,点D在该抛物线上,且点D的横坐标为2,连接BC、BD,设∠OCB=α,∠DBC=β,则cos(α-β)的值是( )
 如图,二次函数y=-$\frac{5}{8}$x2+$\frac{7}{4}$x+3的图象与x轴交于点A、B,与y轴交于点C,点D在该抛物线上,且点D的横坐标为2,连接BC、BD,设∠OCB=α,∠DBC=β,则cos(α-β)的值是( )
如图,二次函数y=-$\frac{5}{8}$x2+$\frac{7}{4}$x+3的图象与x轴交于点A、B,与y轴交于点C,点D在该抛物线上,且点D的横坐标为2,连接BC、BD,设∠OCB=α,∠DBC=β,则cos(α-β)的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
12. 如图,扇形OAB的圆心角的度数为120°,半径长为4,P为弧AB上的动点,PM⊥OA,PN⊥OB,垂足分别为M、N,D是△PMN的外心.当点P运动的过程中,点M、N分别在半径上作相应运动,从点N离开点O时起,到点M到达点O时止,点D运动的路径长为( )
如图,扇形OAB的圆心角的度数为120°,半径长为4,P为弧AB上的动点,PM⊥OA,PN⊥OB,垂足分别为M、N,D是△PMN的外心.当点P运动的过程中,点M、N分别在半径上作相应运动,从点N离开点O时起,到点M到达点O时止,点D运动的路径长为( )
 如图,扇形OAB的圆心角的度数为120°,半径长为4,P为弧AB上的动点,PM⊥OA,PN⊥OB,垂足分别为M、N,D是△PMN的外心.当点P运动的过程中,点M、N分别在半径上作相应运动,从点N离开点O时起,到点M到达点O时止,点D运动的路径长为( )
如图,扇形OAB的圆心角的度数为120°,半径长为4,P为弧AB上的动点,PM⊥OA,PN⊥OB,垂足分别为M、N,D是△PMN的外心.当点P运动的过程中,点M、N分别在半径上作相应运动,从点N离开点O时起,到点M到达点O时止,点D运动的路径长为( )| A. | $\frac{2}{3}$π | B. | π | C. | 2 | D. | 2$\sqrt{3}$ |
18.在下列各数中,$\frac{7}{22}$,$\sqrt{3}$,-2$\frac{1}{2}$,$\root{3}{8}$,是无理数是( )
| A. | $\frac{7}{22}$ | B. | $\sqrt{3}$ | C. | -2$\frac{1}{2}$ | D. | $\root{3}{8}$ |
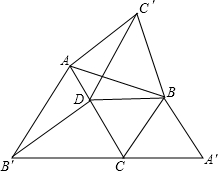 如图,△ABC中,∠ACB=60°,△ABC′,△BCA′,△CAB′都是△ABC形外的等边三角形,点D在边AC 上,且DC=BC.连接DB,DB′,DC′.有下列结论:
如图,△ABC中,∠ACB=60°,△ABC′,△BCA′,△CAB′都是△ABC形外的等边三角形,点D在边AC 上,且DC=BC.连接DB,DB′,DC′.有下列结论: