题目内容
15.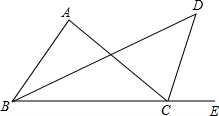 如图,△ABC中,∠ABC的平分线与∠ACE的平分线相交于点D.
如图,△ABC中,∠ABC的平分线与∠ACE的平分线相交于点D.(1)若∠ABC=60°,∠ACB=40°,求∠A和∠D度数.
(2)由第(1)小题的计算,发现∠A和∠D有什么关系.
分析 (1)根据三角形内角和定理,已知∠ABC=60°,∠ACB=40°,易求∠A和∠D度数.
(2)根据三角形内角和定理以及角平分线性质,先求出∠D的等式,再与∠A比较即可解答.
解答 解:(1)在△ABC中,∠ABC=60°,∠ACB=40°,
∴∠A=180°-∠ABC-∠ACB=80°,
∵BD为∠ABC的平分线,CD为∠ACE的平分线,
∴∠DBC=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×60°=30°,∠ACD=$\frac{1}{2}$(180°-∠ACB)=$\frac{1}{2}$×140°=70°,
∴∠D=180°-∠DBC-∠ACB-∠ACD=180°-30°-40°-70°=40°,
∴∠A=80°,∠D=40°.
(2)通过(1)的计算,得到∠A=2∠D,
理由如下:∵∠ACE=∠A+∠ABC,
∴∠ACD+∠ECD=∠A+∠ABD+∠DBE,∠DCE=∠D+∠DBC,
又∵BD平分∠ABC,CD平分∠ACE,
∴∠ABD=∠DBE,∠ACD=∠ECD,
∴∠A=2(∠DCE-∠DBC),∠D=∠DCE-∠DBC,
∴∠A=2∠D.
点评 本题主要考查了三角形内角和定理以及角平分线性质的综合运用,解题时注意:三角形内角和等于180°.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
5. 如图,已知AB⊥BC,垂足为B,AB=3,点P是射线BC上的动点,则线段AP长不可能是( )
如图,已知AB⊥BC,垂足为B,AB=3,点P是射线BC上的动点,则线段AP长不可能是( )
 如图,已知AB⊥BC,垂足为B,AB=3,点P是射线BC上的动点,则线段AP长不可能是( )
如图,已知AB⊥BC,垂足为B,AB=3,点P是射线BC上的动点,则线段AP长不可能是( )| A. | 2.5 | B. | 3 | C. | 4 | D. | 5 |
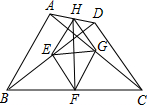 如图,四边形ABCD,AD与BC不平行,AB=CD.AC,BD为四边形ABCD的对角线.E,F,G,H分别是BD,BC,AC,AD的中点.
如图,四边形ABCD,AD与BC不平行,AB=CD.AC,BD为四边形ABCD的对角线.E,F,G,H分别是BD,BC,AC,AD的中点.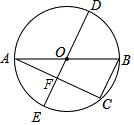 如图,AB是⊙O的直径,AC、BC是⊙O的弦,若点D在优弧ABC上,直径DE⊥AC于点F,AB=8,BC=3,则DF=5.5.
如图,AB是⊙O的直径,AC、BC是⊙O的弦,若点D在优弧ABC上,直径DE⊥AC于点F,AB=8,BC=3,则DF=5.5.