题目内容
3.在△ABC中,∠ACB=90°,AC=BC,点C的坐标为(-1,0),点A的坐标为(-4,2),则B点的坐标为(3,1).分析 作辅助线,构建全等三角形,根据AAS证明△AEC≌△CFB,得AE=CF,EC=BF,根据A(-4,2),C(-1,0)得出线段的长,从而写出点B的坐标.
解答 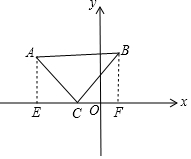 解:如图,过A、B作x轴的垂线,垂足分别为E、F,
解:如图,过A、B作x轴的垂线,垂足分别为E、F,
∴∠AEC=∠CFB=90°,
∴∠EAC+∠ACE=90°,
∵∠ACB=90°,
∴∠ACE+∠BCF=90°,
∴∠EAC=∠BCF,
在△AEC和△CFB中,
∵$\left\{\begin{array}{l}{∠EAC=∠BCF}\\{∠AEC=∠CFB}\\{AC=BC}\end{array}\right.$,
∴△AEC≌△CFB(AAS),
∴AE=CF,EC=BF,
∵A(-4,2),C(-1,0),
∴AE=2,OE=4,OC=1,
∴BF=EC=4-1=3,
CF=AE=2,
∴OF=CF-OC=2-1=1,
∴B(3,1).
故答案为:(3,1).
点评 本题考查了等腰直角三角形的性质、全等三角形的性质和判定、坐标与图形特点,本题能根据AAS证明两三角形全等是关键,利用坐标与图形特点根据坐标写出线段的长,反之,能根据线段的长写出B的坐标,注意象限的符号问题.

练习册系列答案
相关题目
11.下列性质中,矩形具有但菱形不一定具有的是( )
| A. | 对角线互相平分 | B. | 对角线互相垂直 | C. | 对角线相等 | D. | 对边平行 |
8.平面直角坐标系内一点A(2,-5)关于原点对称点的坐标是( )
| A. | (5,-2) | B. | (-2,5) | C. | (-2,-5) | D. | (2,5) |
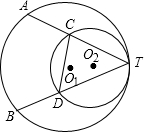 已知:如图,⊙O1与⊙O2内切于点T,⊙O1的弦TA、TB交⊙O2于点C和D,若DC=5,$\frac{TC}{TA}$=$\frac{2}{3}$,求AB的长.
已知:如图,⊙O1与⊙O2内切于点T,⊙O1的弦TA、TB交⊙O2于点C和D,若DC=5,$\frac{TC}{TA}$=$\frac{2}{3}$,求AB的长.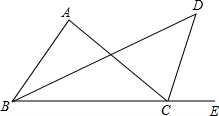 如图,△ABC中,∠ABC的平分线与∠ACE的平分线相交于点D.
如图,△ABC中,∠ABC的平分线与∠ACE的平分线相交于点D.