题目内容
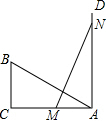如图，在△ABC中，∠C=90°，AB=2，BC=1，射线AD⊥AC，M为AC上的动点，N为射线AD上的动点，点M，N分别在AC，AD上运动，且始终保持MN=AB，当△ABC与△AMN全等时，此时AM的长为（ ）| A、1 | ||
B、
| ||
| C、2 | ||
D、1或
|
考点：全等三角形的性质
专题：
分析：利用勾股定理列式求出AC，然后根据全等三角形对应边相等分情况解答．
解答：解：∵∠C=90°，AB=2，BC=1，
∴AC=
=
=
，
∵△ABC与△AMN全等，
∴AM与BC是对应边时，AM=BC=1，
AM与AC是对应边时，AM=AC=
，
∴AM的长为1或
．
故选D．
∴AC=
| AB2-BC2 |
| 22-12 |
| 3 |
∵△ABC与△AMN全等，
∴AM与BC是对应边时，AM=BC=1，
AM与AC是对应边时，AM=AC=
| 3 |
∴AM的长为1或
| 3 |
故选D．
点评：本题考查了全等三角形的性质，勾股定理，主要利用了全等三角形对应边相等的性质，难点在于要分情况讨论．
练习册系列答案
相关题目
如图，在△ABC中，CD⊥AB于D，tanA=2cos∠BCD．
如图，扇形折扇完全打开后，如果张开的角度（∠BAC）为120°，骨柄AB的长为30cm，扇面的宽度BD的长为20cm，那么这把折扇的扇面面积为（ ）A、
| ||
B、
| ||
C、
| ||
| D、300πcm2 |
已知某种商品的进价为1600元，新年期间，商场为了促销，对该商品按标价的8折出售，仍可获利160元，则该商品的标价应为（ ）
| A、2400元 |
| B、2200元 |
| C、2000元 |
| D、1800元 |
把一个长方形划分成三个全等的长方形，若要使每一个小长方形与原长方形相似，则原长方形的长a与宽b的关系是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|