题目内容
5.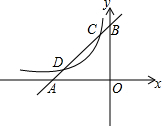 如图所示,已知直线y1=x+m与x轴、y轴分别交于点A,B,与反比例函数y2=$\frac{k}{x}$(x<0)的图象分别交于点C、D,且C的坐标为(-1,2)
如图所示,已知直线y1=x+m与x轴、y轴分别交于点A,B,与反比例函数y2=$\frac{k}{x}$(x<0)的图象分别交于点C、D,且C的坐标为(-1,2)(1)分别求出直线AB与反比例函数的表达式;
(2)求出点D的坐标;
(3)利用图象直接写出:当x在什么范围内取值时y1>y2.
分析 (1)根据待定系数法即可解决.
(2)利用方程组可以求出点D坐标.
(3)观察图象法即可知道答案.
解答 (1)解:∵直线y1=x+m与反比例函数y2=$\frac{k}{x}$(x<0)的图象经过点C(-1,2),
∴2=-1+m,2=-k,
∴m=3,k=-2,
∴直线AB的解析式为y1=x+3,反比例函数解析式为y2=-$\frac{2}{x}$.
(2)由$\left\{\begin{array}{l}{y=-\frac{2}{x}}\\{y=x+3}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.或\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$,
∴点D坐标(-2,1).
(3)由图象可知:-2<x<-1时,y1>y2.
点评 本题考查一次函数、反比例函数的有关知识,解题的关键是会用待定系数法求函数解析式,知道求交点坐标转化为解方程组的思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17. 如图,在?ABCD中,AB=4,AD=2$\sqrt{2}$,E,F分别为边AB,CD上的点,若四边形AECF为正方形,则∠D的度数为( )
如图,在?ABCD中,AB=4,AD=2$\sqrt{2}$,E,F分别为边AB,CD上的点,若四边形AECF为正方形,则∠D的度数为( )
 如图,在?ABCD中,AB=4,AD=2$\sqrt{2}$,E,F分别为边AB,CD上的点,若四边形AECF为正方形,则∠D的度数为( )
如图,在?ABCD中,AB=4,AD=2$\sqrt{2}$,E,F分别为边AB,CD上的点,若四边形AECF为正方形,则∠D的度数为( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
15.估计$\sqrt{7}$+2的值在( )
| A. | 2到3之间 | B. | 3到4之间 | C. | 4到5之间 | D. | 5到6之间 |
 如图,E,F是四边形ABCD的对角线BD上的两点,AB=CD,AD=CB,DF=BE.求证:AE∥CF.
如图,E,F是四边形ABCD的对角线BD上的两点,AB=CD,AD=CB,DF=BE.求证:AE∥CF.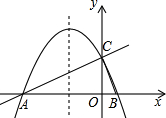 如图,在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$且经过A,C两点,与x轴的另一交点为点B.
如图,在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$且经过A,C两点,与x轴的另一交点为点B.