题目内容
10.研究下列算式:1×3+1=4,2×4+1=9,3×5+1=16,…,你发现的规律是:n(n+2)+1=(n+1)2(n为正整数).分析 观察发现一个正整数乘以比这个正整数大2的数再加1就等于这个正整数加1的平方.
解答 解:∵1×3+1=4=22,
2×4+1=9=32,
3×5+1=16=42,
…,
∴发现的规律是:n(n+2)+1=(n+1)2(n为正整数).
故答案为:n(n+2)+1.
点评 本题考查了规律型:数字的变化类,通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力.本题的规律为等号左边是一个正整数乘以比这个正整数大2的数再加1,等号右边表示的是这个正整数加1的平方.

练习册系列答案
相关题目
1.把多项式5x2y3-2x4y2+7+3x5y按x的降幂排列后,第三项是( )
| A. | 5x2y3 | B. | -2x4y2 | C. | 7 | D. | 3x5y |
2.某商家试销一种成本为50元/件的T恤,经试销发现:每周销售量y(件)与销售单价x(元/件)符合一次函数关系,试销数据如下表:
(1)求y与x的函数关系式;
(2)若该商场前期投资2000元装修门面,则第一周扣除投资和成本后是盈利还是亏损,并求出最多盈利(或最少亏损)多少元?
(3)若在第一周里,按盈利最大(或最少亏损)的销售单价进行销售后,在第二周物价部门进行了干预,规定试销期间单价不低于成本单价,获利又不得高于60%.则该商家经过这两周的营销,要在全部收回投资的基础上使利润达到975元,那么第二周应该确定销售单价为多少元?
| 售价(元/件) | … | 55 | 60 | 70 | … |
| 销量(件) | … | 75 | 70 | 60 | … |
(2)若该商场前期投资2000元装修门面,则第一周扣除投资和成本后是盈利还是亏损,并求出最多盈利(或最少亏损)多少元?
(3)若在第一周里,按盈利最大(或最少亏损)的销售单价进行销售后,在第二周物价部门进行了干预,规定试销期间单价不低于成本单价,获利又不得高于60%.则该商家经过这两周的营销,要在全部收回投资的基础上使利润达到975元,那么第二周应该确定销售单价为多少元?
19.某商场销售A,B两种型号的洗衣机,A型洗衣机的售价为每台1000元,B型洗衣机的售价为每台1500元,某月该商场共销售这两种洗衣机52台,销售额为63000元.为提高销售人员的积极性,商场制定如下工资分配方案:每位销售人员的工资总额=基本工资+奖励工资,每位销售人员的月销售定额为10000元,在销售定额内,得基本工资2500元;超过销售定额,超过部分的销售额按相应比例作为奖励工资.奖励工资发放比例如表1.
(1)该月A,B型号洗衣机各销售多少台?
(2)销售员甲本月领到的工资总额为2990元,请问销售员甲本月的销售额为多少元?
(3)根据我国税法规定,全月工资总额不超过3500元不用缴纳个人所得税:超过3500元的部分为“全月应纳税所得额”,表2是缴纳个人所得税税率表.若销售员乙本月销售A,B两种型号的洗衣机共21台,缴纳个人所得税后实际得到工资3597元.请你求出销售员乙本月销售A型洗衣机多少台?
表1
表2
(1)该月A,B型号洗衣机各销售多少台?
(2)销售员甲本月领到的工资总额为2990元,请问销售员甲本月的销售额为多少元?
(3)根据我国税法规定,全月工资总额不超过3500元不用缴纳个人所得税:超过3500元的部分为“全月应纳税所得额”,表2是缴纳个人所得税税率表.若销售员乙本月销售A,B两种型号的洗衣机共21台,缴纳个人所得税后实际得到工资3597元.请你求出销售员乙本月销售A型洗衣机多少台?
表1
| 销售额 | 奖励工资比例 |
| 超过1万元但不超过1.5万元的部分 | 5% |
| 超过1.5万元但不超过2万元的部分 | 8% |
| 2万元以上的部分 | 10% |
| 全月应纳税所得额 | 税率 |
| 不超过1500元的部分 | 3% |
| 超过1500元至4500元的部分 | 10% |
| … | … |
20.若△ABC的边长分别为a,b,c,则不能确定此三角形是直角三角形的是( )
| A. | a+b+c=12 | B. | ∠A+∠B=∠C | C. | ∠A:∠B:∠C=1:2:3 | D. | a2+b2=c2 |
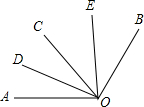 如图,已知∠AOC=60°,∠BOC=70°,且OD平分∠AOC,OE平分∠BOC.
如图,已知∠AOC=60°,∠BOC=70°,且OD平分∠AOC,OE平分∠BOC.