Question

11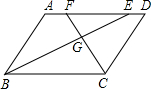．如图，在?ABCD中，BE平分∠ABC，CF平分∠BCD，E、F在AD上，BE与CF相交于点G，若AB=7，BC=10，则△EFG与△BCG的面积之比为（　　）

• A． 4：25
• B． 49：100
• C． 7：10
• D． 2：5

Answer 1

分析 要求△EFG与△BCG的面积之比，只要证明△FGE∽△CGB即可，然后根据面积比等于相似比的平方即可解答本题．

解答 解：∵在?ABCD中，BE平分∠ABC，CF平分∠BCD，
∴AD∥BC，AB=DC，AD=BC，∠CABE=∠CBE，∠DCF=∠BCF，
∴∠AEB=∠CBE，∠DFC=∠BCF，
∴∠ABE=∠AEB，∠DFC=∠DCF，
∴AB=AE，DF=DC，
又∵AB=7，BC=10，
∴AE=DE=7，AD=10，
∴AF=DE=3，
∴FE=4，
∵FE∥BC，
∴△FGE∽△CGB，
∴$\frac{FE}{CB}=\frac{4}{10}=\frac{2}{5}$，
∴$\frac{{S}_{△EFG}}{{S}_{△BCG}}=\frac{4}{25}$，
故选A．

点评 本题考查相似三角形的判定与性质、平行四边形的性质，解题的关键是明确题意，找出所求问题需要的条件．