题目内容
1．已知m、n是方程x2+3x-2=0的两个实数根，则m2+4m+n+2mn的值为（ ）| A． | 1 | B． | 3 | C． | -5 | D． | -9 |
分析 根据根与系数的关系以及一元二次方程的解即可得出m+n=-3、mn=-2、m2+3m=2，将其代入m2+4m+n+2mn中即可求出结论．
解答 解：∵m、n是方程x2+3x-2=0的两个实数根，
∴m+n=-3，mn=-2，m2+3m=2，
∴m2+4m+n+2mn=m2+3m+m+n+2mn=2-3-2×2=-5．
故选C．
点评 本题考查了根与系数的关系以及一元二次方程的解，熟练掌握x1+x2=-$\frac{b}{a}$、x1x2=$\frac{c}{a}$是解题的关键．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
12．等腰三角形的两条边长分别是2cm和5cm，则该三角形的周长为（ ）
| A． | 9cm | B． | 12cm | C． | 9cm或12cm | D． | 7cm |
如图，在半径为R的圆形钢板上，冲去半径为r的四个小圆，若R=8.9cm，r=0.55cm，请你应用所学知识用最简单的方法计算剩余部分面积．（结果保留π）
10．若a=$\frac{3}{8}$x-20，b=$\frac{3}{8}$x-18，c=$\frac{3}{8}$x-16，则a2+b2+c2-ab-ac-bc的值为（ ）
| A． | 12 | B． | 24 | C． | 27 | D． | 54 |
11．
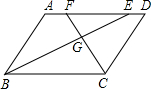如图，在?ABCD中，BE平分∠ABC，CF平分∠BCD，E、F在AD上，BE与CF相交于点G，若AB=7，BC=10，则△EFG与△BCG的面积之比为（ ）
如图，在?ABCD中，BE平分∠ABC，CF平分∠BCD，E、F在AD上，BE与CF相交于点G，若AB=7，BC=10，则△EFG与△BCG的面积之比为（ ）| A． | 4：25 | B． | 49：100 | C． | 7：10 | D． | 2：5 |