题目内容
 如图,顺次连接正方形ABCD的四边中点得到正方形①,再顺次连接正方形①的四边得到正方形②,依此规律继续连接可得到正方形③,正方形④,…
如图,顺次连接正方形ABCD的四边中点得到正方形①,再顺次连接正方形①的四边得到正方形②,依此规律继续连接可得到正方形③,正方形④,…(1)若正方形ABCD的面积为16,则正方形③的边长a3=
(2)若正方形ABCD的面积为S,则正方形n的边长an=
考点:中点四边形
专题:规律型
分析:(1)根据题意,利用中位线定理可证明顺次连接正方形ABCD四边中点得正方形A1B1C1D1的面积为正方形ABCD面积的一半,以此类推可得正方形③的面积,从而求得其边长a3;
(2)根据题意,利用中位线定理可证明顺次连接正方形ABCD四边中点得正方形A1B1C1D1的面积为正方形ABCD面积的一半,以此类推可得正方形n的面积,从而求得其边长an.
(2)根据题意,利用中位线定理可证明顺次连接正方形ABCD四边中点得正方形A1B1C1D1的面积为正方形ABCD面积的一半,以此类推可得正方形n的面积,从而求得其边长an.
解答:解:(1)顺次连接正方形ABCD四边的中点得正方形①,则得正方形①的面积为正方形ABCD面积的一半,即正方形ABCD的
;
顺次连接正方形①的中点得正方形②,则正方形②的面积为正方形①面积的一半,即正方形ABCD的
;
顺次连接正方形②得正方形③,则正方形③的面积为正方形②面积的一半,即正方形ABCD的
.
∵正方形ABCD的面积为16,
∴正方形③的面积是:
×16=2.
∴正方形③的边长a3=
.
故答案是:
;
(2)由(1)的规律知,正方形n的面积是:(
)nS,则正方形n的边长an=
.
故答案是:
.
| 1 |
| 2 |
顺次连接正方形①的中点得正方形②,则正方形②的面积为正方形①面积的一半,即正方形ABCD的
| 1 |
| 4 |
顺次连接正方形②得正方形③,则正方形③的面积为正方形②面积的一半,即正方形ABCD的
| 1 |
| 8 |
∵正方形ABCD的面积为16,
∴正方形③的面积是:
| 1 |
| 8 |
∴正方形③的边长a3=
| 2 |
故答案是:
| 2 |
(2)由(1)的规律知,正方形n的面积是:(
| 1 |
| 2 |
(
|
故答案是:
(
|
点评:本题考查了利用了三角形的中位线的性质,相似图形的面积比等于相似比的平方的性质.进而得到面积关系.

练习册系列答案
相关题目
一次函数y=kx+b的图象经过(-1,m)和(m,1),其中m>1,则k、b的取值范围是( )
| A、k>0且b>0 |
| B、k<0且b>0 |
| C、k>0且b<0 |
| D、k<0且b<0 |
已知a2-2a-3=0,则a2-2a-
的值为( )
| 1 |
| 2a2-4a |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
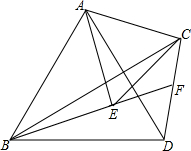 如图,在△ABC中,分别以AB、AC为边作等边△ABD与等边△ACE,连接BE、CD,BE的延长线与CD交于点F,连接AF,有以下四个结论:
如图,在△ABC中,分别以AB、AC为边作等边△ABD与等边△ACE,连接BE、CD,BE的延长线与CD交于点F,连接AF,有以下四个结论: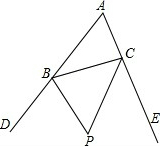 如图,在△ABC中,BP、CP分别是△ABC的外角∠DBC和∠ECB的平分线.
如图,在△ABC中,BP、CP分别是△ABC的外角∠DBC和∠ECB的平分线.