题目内容
1. 如图,AB是⊙O的直径,AF是⊙O切线,CD是垂直于AB的弦,垂足为E,过点C作DA的平行线与AF相交于点F,CD=2$\sqrt{3}$,BE=1.
如图,AB是⊙O的直径,AF是⊙O切线,CD是垂直于AB的弦,垂足为E,过点C作DA的平行线与AF相交于点F,CD=2$\sqrt{3}$,BE=1.求证:
(1)四边形FADC是菱形;
(2)FC是⊙O的切线.
分析 (1)首先连接OC,由垂径定理,可求得CE的长,又由勾股定理,可求得半径OC的长,然后由勾股定理求得AD的长,即可得AD=CD,易证得四边形FADC是平行四边形,继而证得四边形FADC是菱形;
(2)首先连接OF,易证得△AFO≌△CFO,继而可证得FC是⊙O的切线.
解答 证明:(1)连接OC,
∵AB是⊙O的直径,CD⊥AB,
∴CE=DE=$\frac{1}{2}$CD=$\frac{1}{2}$×2$\sqrt{3}$=$\sqrt{3}$,
设OC=x,
∵BE=2,
∴OE=x-2,
在Rt△OCE中,OC2=OE2+CE2,
∴x2=(x-1)2+($\sqrt{3}$)2,
解得:x=2,
∴OA=OC=2,OE=2,
∴AE=3,
在Rt△AED中,AD=$\sqrt{A{E}^{2}+D{E}^{2}}$=2$\sqrt{3}$,
∴AD=CD,
∵AF是⊙O切线,
∴AF⊥AB,
∵CD⊥AB,
∴AF∥CD,
∵CF∥AD,
∴四边形FADC是平行四边形,
∵AD=CD,
∴平行四边形FADC是菱形;
(2)连接OF,AC,
∵四边形FADC是菱形,
∴FA=FC,
∴∠FAC=∠FCA,
∵AO=CO,
∴∠OAC=∠OCA,
∴∠FAC+∠OAC=∠FCA+∠OCA,
即∠OCF=∠OAF=90°,
即OC⊥FC,
∵点C在⊙O上,
∴FC是⊙O的切线.
点评 此题考查了切线的判定与性质、菱形的判定与性质、垂径定理、勾股定理以及全等三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
11.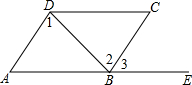 如图,已知AD∥BC,下列结论不一定正确的是( )
如图,已知AD∥BC,下列结论不一定正确的是( )
 如图,已知AD∥BC,下列结论不一定正确的是( )
如图,已知AD∥BC,下列结论不一定正确的是( )| A. | ∠A+∠ABC=180° | B. | ∠1=∠2 | C. | ∠A=∠3 | D. | ∠C=∠3 |
12.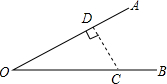 如图,∠O=30°,C为OB上一点,且OC=8,以点C为圆心,半径为4的圆与直线OA的位置关系是( )
如图,∠O=30°,C为OB上一点,且OC=8,以点C为圆心,半径为4的圆与直线OA的位置关系是( )
 如图,∠O=30°,C为OB上一点,且OC=8,以点C为圆心,半径为4的圆与直线OA的位置关系是( )
如图,∠O=30°,C为OB上一点,且OC=8,以点C为圆心,半径为4的圆与直线OA的位置关系是( )| A. | 相离 | B. | 相交 | ||
| C. | 相切 | D. | 以上三种情况均有可能 |
16.森林是地球之肺,每年能为人类提供大约29.3亿吨的有机物,29.3亿吨用科学记数法表示为( )
| A. | 29.3×107 | B. | 2.93×108 | C. | 0.293×1010 | D. | 2.93×109 |
13.下列图形中,只是中心对称图形而不是轴对称图形的是( )
| A. |  等边三角形 | B. |  平行四边形 | C. |  正六边形 | D. |  扇形 |
10.在慈心一日捐活动中,我校某小组7名同学积极捐出自己的零花钱,他们捐款的数额分别是(单位:元):80,20,80,40,80,25,135.这组数据的众数和中位数分别是( )
| A. | 80,20 | B. | 80,40 | C. | 80,80 | D. | 135,80 |