题目内容
3. 如图,O是线段AB的中点,C在线段OB上,AC=6,CB=3,则OC的长等于( )
如图,O是线段AB的中点,C在线段OB上,AC=6,CB=3,则OC的长等于( )| A. | 0.5 | B. | 1 | C. | 1.5 | D. | 2 |
分析 首先根据AC=6,CB=3,求出AB的长度是多少;然后用它除以2,求出AO的长度是多少;最后用AC的长度减去AO的长度,求出OC的长等于多少即可.
解答 解:∵AC=6,CB=3,
∴AB=6+3=9,
∵O是线段AB的中点,
∴AO=9÷2=4.5,
∴OC=AC-AO=6-4.5=1.5.
故选:C.
点评 此题主要考查了两点间的距离的含义和求法,以及线段的中点的性质和应用,要熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.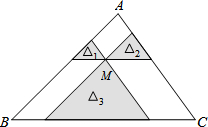 如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1,△2,△3(图中阴影部分)的面积分别是4,9和16,则△ABC的面积是( )
如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1,△2,△3(图中阴影部分)的面积分别是4,9和16,则△ABC的面积是( )
 如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1,△2,△3(图中阴影部分)的面积分别是4,9和16,则△ABC的面积是( )
如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1,△2,△3(图中阴影部分)的面积分别是4,9和16,则△ABC的面积是( )| A. | 49 | B. | 64 | C. | 100 | D. | 81 |
18.将一副三角板按如图①的位置摆放,将△DEF绕点A(F)逆时针旋转60°后,得到如图②,测得CG=6$\sqrt{2}$,则AC长是( )
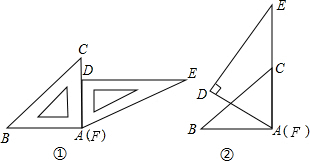

| A. | 6+2$\sqrt{3}$ | B. | 9 | C. | 10 | D. | 6+6$\sqrt{2}$ |
13. 如图,AD=DF=FB,DE∥FG∥BC,且把三角形ABC分成面积为S1,S2,S3三部分,则S1:S2:S3=( )
如图,AD=DF=FB,DE∥FG∥BC,且把三角形ABC分成面积为S1,S2,S3三部分,则S1:S2:S3=( )
 如图,AD=DF=FB,DE∥FG∥BC,且把三角形ABC分成面积为S1,S2,S3三部分,则S1:S2:S3=( )
如图,AD=DF=FB,DE∥FG∥BC,且把三角形ABC分成面积为S1,S2,S3三部分,则S1:S2:S3=( )| A. | 1:2:3 | B. | 1:4:9 | C. | 1:3:5 | D. | 无法确定 |
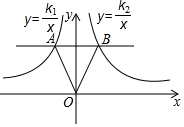 如图,在x轴上方,平行于x轴的直线与反比例函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$的图象分别交于A、B两点,连接OA、OB,若△AOB的面积为6,则k1-k2=-12.
如图,在x轴上方,平行于x轴的直线与反比例函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$的图象分别交于A、B两点,连接OA、OB,若△AOB的面积为6,则k1-k2=-12. 如图,各图中的阴影部分绕轴旋转一周,所形成的立体图形分别是圆柱、圆锥、球.
如图,各图中的阴影部分绕轴旋转一周,所形成的立体图形分别是圆柱、圆锥、球. 如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD、OD.
如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD、OD.