题目内容
7.某玩具厂生产一种玩具,本着控制固定成本,降价促销的原则,使生产的玩具能够全部售出.据市场调查,若按每个玩具280元销售时,每月可销售300个.若销售单价每降低1元,每月可多售出2个.据统计,每个玩具的固定成本Q(元)与月产销量y(个)满足如下关系:| 月产销量y(个) | … | 160 | 200 | 240 | 300 | … |
| 每个玩具的固定成本Q(元) | … | 60 | 48 | 40 | 32 | … |
(2)若每个玩具的固定成本为30元,求它的销售单价是多少元?
(3)若该厂这种玩具的月产销量不超过400个,求此时销售单价最低为多少元?
分析 (1)设y=kx+b,把(280,300),(279,302)代入解方程组即可;观察函数表可知两个变量的乘积为定值,所以固定成本Q(元)与月产销量y(个)之间存在反比例函数关系,不妨设Q=$\frac{m}{x}$,由此即可解决问题.
(2)求出销售价即可解决问题.
(3)根据条件分别列出不等式即可解决问题.
解答 解;(1)由于销售单价每降低1元,每月可多售出2个,所以月产销量y(个)与销售单价x (元)之间存在一次函数关系,不妨设y=kx+b,则(280,300),(279,302)满足函数关系式,得 $\left\{\begin{array}{l}{280k+b=300}\\{279k+b=302}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{k=-2}\\{b=860}\end{array}\right.$,
产销量y(个)与销售单价x (元)之间的函数关系式为y=-2x+860.
观察函数表可知两个变量的乘积为定值,所以固定成本Q(元)与月产销量y(个)之间存在反比例函数关系,不妨设Q=$\frac{m}{x}$,将Q=60,y=160代入得到m=9600,
此时Q=$\frac{9600}{x}$.
(2)当Q=30时,y=320,由(1)可知y=-2x+860,所以x=270,即销售单价为270元,
由于$\frac{30}{270}$=$\frac{1}{9}$,
∴成本占销售价的$\frac{1}{9}$.
(3)若y≤400,则Q≥$\frac{9600}{400}$,即Q≥24,固定成本至少是24元,
400≥-2x+860,解得x≥230,即销售单价最低为230元.
点评 本题考查一次函数的应用、不等式,成本,销售价、销售量之间的关系,解题的关键是理解题意,灵活应用待定系数法解决问题,属于中考常考题型.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案| A. | $\frac{720}{48+x}$-$\frac{720}{x}$=5 | B. | $\frac{720}{48}$+5=$\frac{720}{48+x}$ | C. | $\frac{720}{48}$-$\frac{720}{x}$=5 | D. | $\frac{720}{48}$-$\frac{720}{48+x}$=5 |
| A. | 22.34×105 | B. | 2.234×105 | C. | 2.234×106 | D. | 0.2234×107 |
 如图,在Rt△ABC中,∠ACB=90°,AC=BC,点M在AC边上,且AM=1,MC=4,动点P在AB边上,连接PC,PM,则PC+PM的最小值是( )
如图,在Rt△ABC中,∠ACB=90°,AC=BC,点M在AC边上,且AM=1,MC=4,动点P在AB边上,连接PC,PM,则PC+PM的最小值是( )| A. | $\sqrt{17}$ | B. | 6 | C. | $\sqrt{26}$ | D. | 7 |
甲:根据一个数的平方是非负数可知(a-b)2≥0,
∴a2-2ab+b2≥0,
∴a2+b2≥2ab.
乙:如图1,两个正方形的边长分别为a、b(b≤a),如图2,先将边长为a的正方形沿虚线部分分别剪成Ⅰ、Ⅱ、Ⅲ三部分,若再将Ⅰ、Ⅱ和边长为b的正方形拼接成如图3所示的图形,可知此时图3的面积为2ab,其面积小于或等于原来两个正方形的面积和,故不等式a2+b2≥2ab成立.
则对于两人的作业,下列说法正确的是( )
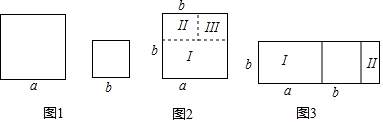
| A. | 甲、乙都对 | B. | 甲对,乙不对 | C. | 甲不对,乙对 | D. | 甲、乙都不对 |
| A. | 2×103 | B. | 2×104 | C. | 20×103 | D. | 0.2×103 |
| A. | a>0 | B. | a<0 | C. | a>-$\frac{1}{2}$ | D. | a<-$\frac{1}{2}$ |
 已知如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,不等式ax+b>$\frac{k}{x}$的解集为( )
已知如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,不等式ax+b>$\frac{k}{x}$的解集为( )| A. | x<-3 | B. | x<-3或x>1 | C. | -3<x<0或x>1 | D. | -3<x<1 |
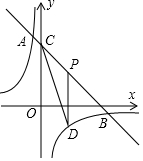 如图,直线y=-x+8与双曲线y=$\frac{k}{x}$相交于A,B两点,与y轴交于点C,点P是线段BC上的动点(点P不与点B,C重合),过P作y轴的平行线,交双曲线于点D,连接CD,若点A的横坐标为-1,则△PDC的面积的最大值为$\frac{25}{2}$.
如图,直线y=-x+8与双曲线y=$\frac{k}{x}$相交于A,B两点,与y轴交于点C,点P是线段BC上的动点(点P不与点B,C重合),过P作y轴的平行线,交双曲线于点D,连接CD,若点A的横坐标为-1,则△PDC的面积的最大值为$\frac{25}{2}$.