题目内容
20.已知N=$\root{3}{4}$+$\root{3}{2}$+1,求$\frac{1}{N}$的值.分析 设$\root{3}{2}$=t,则$\root{3}{4}$=t2,N=t2+t+1,依此得到$\frac{1}{N}$=$\frac{1}{{t}^{2}+t+1}$,再根据分式的基本性质和立方公式得到原式=$\frac{t-1}{{t}^{3}-1}$,再代入计算即可求解.
解答 解:设$\root{3}{2}$=t,则$\root{3}{4}$=t2,N=t2+t+1,
则$\frac{1}{N}$=$\frac{1}{{t}^{2}+t+1}$
=$\frac{t-1}{({t}^{2}+t+1)(t-1)}$
=$\frac{t-1}{{t}^{3}-1}$
=$\frac{\root{3}{2}-1}{2-1}$
=$\root{3}{2}$-1.
点评 考查了立方公式,换元思想的运用,关键是根据立方公式得到$\frac{1}{N}$=$\frac{\root{3}{2}-1}{2-1}$.其中立方公式:(a±b)3=a3±3a2b+3ab2±b3.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
10.下列运算正确的是( )
| A. | (a-b)2=a2-b2 | B. | 3a2-2a2=a2 | C. | -2(a-1)=-2a-1 | D. | a6÷a3=a2 |
 在△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是AB的中点,求∠ECD的度数.
在△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是AB的中点,求∠ECD的度数.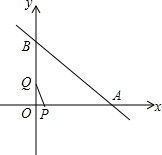 如图,直线y=-x+8与x轴、y轴交于A、B两点,点P、点Q同时从点O出发,分别以每秒3个单位和每秒4个单位的速度沿x轴、y轴方向移动,连接PQ.设移动的时间为t秒(0<t<2),以点P为中心,顺时针旋转△POQ,使旋转后的△O′PQ′的边PQ′恰好落在x轴上.
如图,直线y=-x+8与x轴、y轴交于A、B两点,点P、点Q同时从点O出发,分别以每秒3个单位和每秒4个单位的速度沿x轴、y轴方向移动,连接PQ.设移动的时间为t秒(0<t<2),以点P为中心,顺时针旋转△POQ,使旋转后的△O′PQ′的边PQ′恰好落在x轴上.  如图所示,三角形ABC是通过平移三角形DEF得到的,已知ED和BA是对应线段,请在图中画出三角形DEF.
如图所示,三角形ABC是通过平移三角形DEF得到的,已知ED和BA是对应线段,请在图中画出三角形DEF.