题目内容
11. 在△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是AB的中点,求∠ECD的度数.
在△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是AB的中点,求∠ECD的度数.
分析 先求出∠BCD和∠ACD,再根据直角三角形两锐角互余求出∠B,根据直角三角形斜边上的中线等于斜边的一半可得CE=BE,根据等边对等角可得∠BCE=∠B,再求出∠ECD=45°.
解答 解:∵∠ACB=90°,∠ACD=3∠BCD,
∴∠BCD=90°×$\frac{1}{1+3}$=22.5°,
∠ACD=90°×$\frac{3}{1+3}$=67.5°,
∵CD⊥AB,
∴∠B=90°-22.5°=67.5°,
∵E是AB的中点,∠ACB=90°,
∴CE=BE,
∴∠BCE=∠B=67.5°,
∴∠ECD=∠BCE-∠BCD=67.5°-22.5°=45°.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形的性质,熟记性质并准确识图,理清图中各角度之间的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.已知反比例函数图象经过点(1,-1),(m,1),则m等于( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
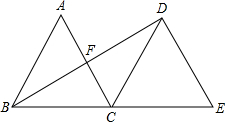 如图,△ABC是边长为2的等边三角形,将△ABC沿直线BC平移到△DCE的位置,连接BD,求△ABC平移的距离和BD的长.
如图,△ABC是边长为2的等边三角形,将△ABC沿直线BC平移到△DCE的位置,连接BD,求△ABC平移的距离和BD的长.
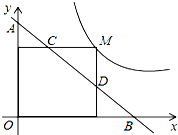 如图,M为双曲线y=$\frac{2}{3x}$(x>0)上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于点D、C两点.若直线y=-x+m与y轴交于点A,与x轴交于点B,则AD•BC的值为$\frac{4}{3}$.
如图,M为双曲线y=$\frac{2}{3x}$(x>0)上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于点D、C两点.若直线y=-x+m与y轴交于点A,与x轴交于点B,则AD•BC的值为$\frac{4}{3}$.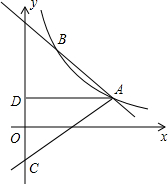 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(2$\sqrt{3}$,1),直线AB与反比例函数图象交与另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(2$\sqrt{3}$,1),直线AB与反比例函数图象交与另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.