ЬтФПФкШн
ЁОЬтФПЁПШчЭМЂйЃЌОиаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌНЋ
ЃЌНЋ![]() ШЦЕу
ШЦЕу![]() Дг
Дг![]() ДІПЊЪМАДЫГЪБеыЗНЯђа§зЊЃЌ
ДІПЊЪМАДЫГЪБеыЗНЯђа§зЊЃЌ![]() НЛБп
НЛБп![]() ЃЈЛђ
ЃЈЛђ![]() ЃЉгкЕу
ЃЉгкЕу![]() ЃЌ
ЃЌ![]() НЛБп
НЛБп![]() ЃЈЛђ
ЃЈЛђ![]() ЃЉгкЕу
ЃЉгкЕу![]() .ЕБ
.ЕБ![]() а§зЊжС
а§зЊжС![]() ДІЪБЃЌ
ДІЪБЃЌ![]() ЕФа§зЊЫцМДЭЃжЙ.
ЕФа§зЊЫцМДЭЃжЙ.
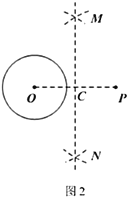
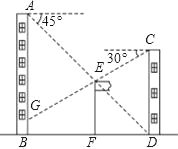
ЃЈ1ЃЉЬиЪтЧщаЮЃКШчЭМЂкЃЌЗЂЯжЕБ![]() Й§Еу
Й§Еу![]() ЪБЃЌ
ЪБЃЌ![]() вВЧЁКУЙ§Еу
вВЧЁКУЙ§Еу![]() ЃЌДЫЪБ
ЃЌДЫЪБ![]() ЪЧЗёгы
ЪЧЗёгы![]() ЯрЫЦЃПВЂЫЕУїРэгЩЃЛ
ЯрЫЦЃПВЂЫЕУїРэгЩЃЛ
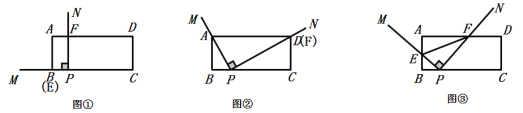
ЃЈ2ЃЉРрБШЬНОПЃКШчЭМЂлЃЌдка§зЊЙ§ГЬжаЃЌ![]() ЕФжЕЪЧЗёЮЊЖЈжЕЃПШєЪЧЃЌЧыЧѓГіИУЖЈжЕЃЛШєВЛЪЧЃЌЧыЫЕУїРэгЩЃЛ
ЕФжЕЪЧЗёЮЊЖЈжЕЃПШєЪЧЃЌЧыЧѓГіИУЖЈжЕЃЛШєВЛЪЧЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЭиеЙбгЩьЃКЩш![]() ЪБЃЌ
ЪБЃЌ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЪдгУКЌ
ЃЌЪдгУКЌ![]() ЕФДњЪ§ЪНБэЪО
ЕФДњЪ§ЪНБэЪО![]() ЃЛ
ЃЛ
Ђйдка§зЊЙ§ГЬжаЃЌШє![]() ЪБЃЌЧѓЖдгІЕФ
ЪБЃЌЧѓЖдгІЕФ![]() ЕФУцЛ§ЃЛ
ЕФУцЛ§ЃЛ
Ђкдка§зЊЙ§ГЬжаЃЌЕБ![]() ЕФУцЛ§ЮЊ4.2ЪБЃЌЧѓЖдгІЕФ
ЕФУцЛ§ЮЊ4.2ЪБЃЌЧѓЖдгІЕФ![]() ЕФжЕ.
ЕФжЕ.
ЁОД№АИЁПЃЈ1ЃЉЯрЫЦЃЛЃЈ2ЃЉЖЈжЕЃЌ![]() ЃЛЃЈ3ЃЉЂй2ЃЌЂк
ЃЛЃЈ3ЃЉЂй2ЃЌЂк![]() .
.
ЁОНтЮіЁП
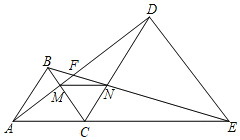
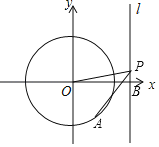
ЃЈ1ЃЉИљОнЁАСННЧЯрЕШЕФСНИіШ§НЧаЮЯрЫЦЁБМДПЩЕУГіД№АИЃЛ
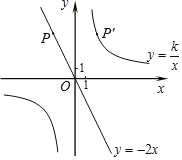
ЃЈ2ЃЉгЩ![]() ЕУГі
ЕУГі![]() ЃЌгж
ЃЌгж![]() ЮЊЖЈжЕЃЌМДПЩЕУГіД№АИЃЛ
ЮЊЖЈжЕЃЌМДПЩЕУГіД№АИЃЛ
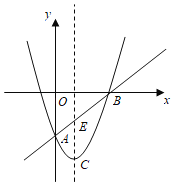
ЃЈ3ЃЉЯШЩш![]() НсКЯ
НсКЯ![]() ЕУГі
ЕУГі
![]() ЂйНЋt=1ДњШы
ЂйНЋt=1ДњШы![]() жаЧѓНтМДПЩЕУГіД№АИЃЛ
жаЧѓНтМДПЩЕУГіД№АИЃЛ
ЂкНЋs=4.2ДњШы![]() жаЧѓНтМДПЩЕУГіД№АИ.
жаЧѓНтМДПЩЕУГіД№АИ.
ЃЈ1ЃЉЯрЫЦ
РэгЩЃКЁп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
гжЁп![]() ЃЌ
ЃЌ
Ёр![]() ЃЛ
ЃЛ
ЃЈ2ЃЉ
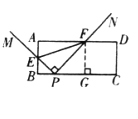
дка§зЊЙ§ГЬжа![]() ЕФжЕЮЊЖЈжЕЃЌ
ЕФжЕЮЊЖЈжЕЃЌ
РэгЩШчЯТЃКЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌЁп
ЃЌЁп![]() ЃЌ
ЃЌ
![]() ЃЌЁр
ЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
ЁпЫФБпаЮ![]() ЮЊОиаЮЃЌЁрЫФБпаЮ
ЮЊОиаЮЃЌЁрЫФБпаЮ![]() ЮЊОиаЮЃЌ
ЮЊОиаЮЃЌ
Ёр![]()
Ёр![]()
МДдка§зЊЙ§ГЬжаЃЌ![]() ЕФжЕЮЊЖЈжЕЃЌ
ЕФжЕЮЊЖЈжЕЃЌ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉгЩЃЈ2ЃЉжЊЃК![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
гжЁп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]()
![]()
МДЃК![]() ЃЛ
ЃЛ
ЂйЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФУцЛ§
ЕФУцЛ§![]() ЃЌ
ЃЌ
ЂкЕБ![]() ЪБЃЌЁр
ЪБЃЌЁр![]()
НтЕУЃК![]() ЃЌ
ЃЌ![]() ЃЈЩсШЅЃЉ
ЃЈЩсШЅЃЉ
ЁрЕБ![]() ЕФУцЛ§ЮЊ4.2ЪБЃЌ
ЕФУцЛ§ЮЊ4.2ЪБЃЌ![]() ЃЛ
ЃЛ

ЁОЬтФПЁПФГЬьЩЯЮч7ЃК30ЃЌаЁЗМдкМвЭЈЙ§ЕЮЕЮДђГЕШэМўДђГЕЧАЭљЖЏГЕеОДюГЫЕБЬьЩЯЮч8ЃК30ЕФЖЏГЕЃЎМЧЦћГЕЕФааЪЛЪБМфЮЊtаЁЪБЃЌааЪЛЫйЖШЮЊvЧЇУз/аЁЪБЃЈЦћГЕааЪЛЫйЖШВЛГЌЙ§60ЧЇУз/аЁЪБЃЉЃЎИљОнОбщЃЌvЃЌtЕФвЛзщЖдгІжЕШчЯТБэЃК
VЃЈЧЇУз/аЁЪБЃЉ | 20 | 30 | 40 | 50 | 60 |
TЃЈаЁЪБЃЉ | 0.6 | 0.4 | 0.3 | 0.25 | 0.2 |
ЃЈ1ЃЉИљОнБэжаЕФЪ§ОнУшЕуЃЌЧѓГіЦНОљЫйЖШvЃЈЧЇУз/аЁЪБЃЉЙигкааЪЛЪБМфtЃЈаЁЪБЃЉЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉШєаЁЗМДгПЊЪМДђГЕЕНЩЯГЕгУСЫ10ЗжжгЃЌаЁЗМЯыдкЖЏГЕГіЗЂЧААыаЁЪБЕНДяЖЏГЕеОЃЌШєЦћГЕЕФЦНОљЫйЖШЮЊ32ЧЇУз/аЁЪБЃЌаЁЗМФмЗёдкдЄЖЈЕФЪБМфФкЕНДяЖЏГЕеОЃПЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєЦћГЕЕНДяЖЏГЕеОЕФааЪЛЪБМфtТњзу0.3ЃМtЃМ0.5ЃЌЧѓЦНОљЫйЖШvЕФШЁжЕЗЖЮЇЃЎ