Question

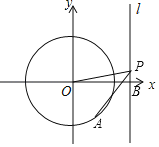
【题目】已知点A是圆心为坐标原点O且半径为3的圆上的动点，经过点B（4，0）作直线l⊥x轴，点P是直线l上的动点，若∠OPA＝45°，则△BOP的面积的最大值为_____．

Answer 1

【答案】2

【解析】

当PA是⊙O的切线时，OP最长，则PB最长，故△BOP的面积的最大，连接OA，根据切线的性质和已知条件得出△OPA是等腰直角三角形，利用勾股定理确定OP，进而求得PB，根据三角形面积公式即可求得．

当PA是⊙O的切线时，OP最长，则PB最长，故△BOP的面积的最大，连接OA，

∵PA是⊙O的切线，

∴OA⊥PA，

∵∠OPA＝45°，

∴△OPA是等腰直角三角形，

∴OA＝PA＝3，

∴OP＝3，

在Rt△BOP中，PB＝＝＝，

∴△BOP的面积的最大值为×4×＝2，

故答案为：2．