题目内容
 如图所示,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4,BC=7,DC=5,点P在BC上移动,则当PA+PD取最小值时,△APD中边AP上的高为( )
如图所示,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4,BC=7,DC=5,点P在BC上移动,则当PA+PD取最小值时,△APD中边AP上的高为( )A、2
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:轴对称-最短路线问题
专题:
分析:要求△APD中边AP上的高,根据三角形的面积,由勾股定理即可得解.
解答: 解:过点D作DE⊥BC于E,
解:过点D作DE⊥BC于E,
∵AD∥BC,AB⊥BC,
∴四边形ABED是矩形,
∴BE=AD=4,
∵BC=7,
∴EC=3,
∵DC=5,
∴DE=
=4,
∴AB=DE=4,
延长AB到A′,使得A′B=AB,连接A′D交BC于P,此时PA+PD最小,
∴△A′PB≌△DPE,
∴BP=EP,
∴PA=PD,
∴BP=
AD=2,
∴AP=
=2
,
在△APD中,由面积公式可得
△APD中边AP上的高=4×4÷2
=
.
故选C.
 解:过点D作DE⊥BC于E,
解:过点D作DE⊥BC于E,∵AD∥BC,AB⊥BC,
∴四边形ABED是矩形,
∴BE=AD=4,
∵BC=7,
∴EC=3,
∵DC=5,
∴DE=
| DC2-EC2 |
∴AB=DE=4,
延长AB到A′,使得A′B=AB,连接A′D交BC于P,此时PA+PD最小,
∴△A′PB≌△DPE,
∴BP=EP,
∴PA=PD,
∴BP=
| 1 |
| 2 |
∴AP=
| AB2+BP2 |
| 5 |
在△APD中,由面积公式可得
△APD中边AP上的高=4×4÷2
| 5 |
8
| ||
| 5 |
故选C.
点评:此题综合性较强,考查了梯形一般辅助线的作法、勾股定理、三角形的面积计算等知识点.

练习册系列答案
相关题目
下列4个命题:①矩形的对角线互相平分且相等;②对角线互相垂直的四边形是菱形;③等腰梯形的两条对角线相等;④等腰三角形底边上的中点到两腰的距离相等.其中正确的是( )
| A、①②③ | B、②③④ |
| C、①②④ | D、①③④ |
把方程4y+
=1+x写成用含x的代数式表示y的形式,以下各式正确的是( )
| x |
| 3 |
A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=
|
用配方法解一元二次方程x2+4x-5=0,此方程可变形为( )
| A、(x-2)2=9 |
| B、(x+2)2=9 |
| C、(x+2)2=1 |
| D、(x-2)2=1 |
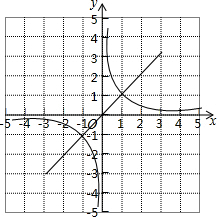 如图是函数y=x与y=
如图是函数y=x与y=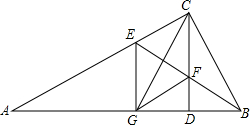 Rt△ABC中,CD是斜边AB上的高,BE平分∠CBA交AC于E,交CD于F,CG⊥BE交AB于G.
Rt△ABC中,CD是斜边AB上的高,BE平分∠CBA交AC于E,交CD于F,CG⊥BE交AB于G.
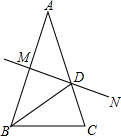 如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M,
如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M,