题目内容
 如图△ABC内接于⊙O,AD平分∠BAC,交⊙O于点K,过点A作⊙O的切线交CB的延长线于点E
如图△ABC内接于⊙O,AD平分∠BAC,交⊙O于点K,过点A作⊙O的切线交CB的延长线于点E(1)求证:∠EAB=∠ACE;
(2)连接BD,若∠E=∠DAB,
| BK |
| BD |
| 3 |
| 5 |
| 5 |
考点:切线的性质
专题:
分析:(1)过A作⊙O的直径,交⊙O于F,连接CF,由圆周角定理和切线的性质可证得结论;
(2)连接CD交AF于G,由条件可证明△ABK∽△CDK∽△ADC,且都是等腰三角形,利用相似三角形的性质可求得CD,进一步可求得AF,可求得半径.
(2)连接CD交AF于G,由条件可证明△ABK∽△CDK∽△ADC,且都是等腰三角形,利用相似三角形的性质可求得CD,进一步可求得AF,可求得半径.
解答:(1)证明:如图1,过A作⊙O的直径,交⊙O于F,连接CF,

∵AF是直径,
∴∠ACF=90°,即∠ACB+∠BCF=90°,
∵∠BAF与∠BCF同弧BF,
∴∠BAF=∠BCF,
∴∠ACE+∠BAF=90°
∵AE为⊙O的切线,
∴∠EAB+∠BAF=90°,
∴∠EAB=∠ACE;
(2)解:如图2,连接CD交AF于G,
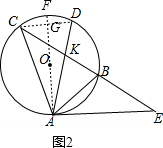
∵AD平分∠BAC,∠E=∠BAD,
∴BD=CD,∠BAD=∠DAC=∠E,
∵∠EAB=∠ACE,
而∠BAK=∠EAB+∠BAD,∠AKB=∠ACB+∠KAC,
∴∠BAK=∠AKB,即△ABK是等腰三角形,
∵∠ABC和∠ADC同弧AC,
∴∠ABC=∠ADC,
∴△ABK∽△CDK∽△ADC,且都是等腰三角形,
∴CK=CD=BD,AD=AC,
∵
=
,
∴
=
=
,
∵DK=2
,
∴AK=3
,AD=5
,
∵
=
∴CD=5
∵△ADC是等腰三角形,AF是直径,
∴AF⊥CD,CG=DG=
,
∴根据勾股定理AG=
,
∵△AFC∽△ACG,
∴
=
,
∴AF=
,
∴⊙O的半径为
.

∵AF是直径,
∴∠ACF=90°,即∠ACB+∠BCF=90°,
∵∠BAF与∠BCF同弧BF,
∴∠BAF=∠BCF,
∴∠ACE+∠BAF=90°
∵AE为⊙O的切线,
∴∠EAB+∠BAF=90°,
∴∠EAB=∠ACE;
(2)解:如图2,连接CD交AF于G,

∵AD平分∠BAC,∠E=∠BAD,
∴BD=CD,∠BAD=∠DAC=∠E,
∵∠EAB=∠ACE,
而∠BAK=∠EAB+∠BAD,∠AKB=∠ACB+∠KAC,
∴∠BAK=∠AKB,即△ABK是等腰三角形,
∵∠ABC和∠ADC同弧AC,
∴∠ABC=∠ADC,
∴△ABK∽△CDK∽△ADC,且都是等腰三角形,
∴CK=CD=BD,AD=AC,
∵
| BK |
| BD |
| 3 |
| 5 |
∴
| AK |
| AD |
| BK |
| CD |
| 3 |
| 5 |
∵DK=2
| 5 |
∴AK=3
| 5 |
| 5 |
∵
| CD |
| DK |
| AD |
| CD |
∴CD=5
| 2 |
∵△ADC是等腰三角形,AF是直径,
∴AF⊥CD,CG=DG=
5
| ||
| 2 |
∴根据勾股定理AG=
15
| ||
| 2 |
∵△AFC∽△ACG,
∴
| AF |
| AC |
| AC |
| AG |
∴AF=
25
| ||
| 3 |
∴⊙O的半径为
25
| ||
| 6 |
点评:本题主要考查切线的性质及圆周角定理、相似三角形的判定和性质,在(1)中作出过A的直径,构造垂直找到角之间的关系,在(2)中作出直径证明△ABK∽△CDK∽△ADC,且都是等腰三角形,求得AF是解题的关键.

练习册系列答案
相关题目
把方程4y+
=1+x写成用含x的代数式表示y的形式,以下各式正确的是( )
| x |
| 3 |
A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=
|

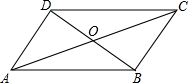 如图所示,在?ABCD中,AD⊥BD,AD=4,OD=3.
如图所示,在?ABCD中,AD⊥BD,AD=4,OD=3. 已知如图,四边形ABCD的边长是2的菱形,且∠CDA=30°,CF⊥x轴,求点D关于CF的对称点D′的坐标.
已知如图,四边形ABCD的边长是2的菱形,且∠CDA=30°,CF⊥x轴,求点D关于CF的对称点D′的坐标.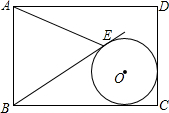 如图,在矩形ABCD中,AB=3,AD=4,⊙O与边BC,CD相切,现有一条过点B的直线与⊙O相切于点E,连接BE,△ABE恰为等边三角形,则⊙O的半径为
如图,在矩形ABCD中,AB=3,AD=4,⊙O与边BC,CD相切,现有一条过点B的直线与⊙O相切于点E,连接BE,△ABE恰为等边三角形,则⊙O的半径为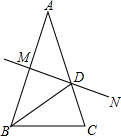 如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M,
如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M, 如图所示,在平面直角坐标系xOy中,已知P,Q两点的纵坐标分别为6,2,直线PQ与x轴所成锐角为30°.
如图所示,在平面直角坐标系xOy中,已知P,Q两点的纵坐标分别为6,2,直线PQ与x轴所成锐角为30°. 如图,AP∥BC,∠ABC的平分线交AC于点O,交AP于点P,且∠BAC=80°,∠P=35°,求∠C的度数.
如图,AP∥BC,∠ABC的平分线交AC于点O,交AP于点P,且∠BAC=80°,∠P=35°,求∠C的度数.