题目内容
点M(2，-3）与点N（2，3）关于______对称；点A(-2，-4）与点B（2，4）关于______对称；点G(4，0）与点H（-4，0）关于____________对称.
x轴 原点 y轴
【解析】根据关于x轴对称的点的坐标规律:横坐标相同,纵坐标互为相反数,关于原点的对称点,横纵坐标都变成相反数,关于y轴对称的点的坐标规律:横坐标互为相反数,纵坐标相同,
所以点M与点N关于x轴对称,点A与点B关于原点对称,点G与点H关于y轴对称,故答案为: x轴, 原点, y轴.
练习册系列答案
阅读快车系列答案
相关题目
在等边△ABC中，CD是∠ACB的平分线，过D作DE∥BC交AC于E，若△ABC的边长为a，则△ADE的周长为 ( )
A. 2a B.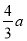 
C. 1．5a D. a
C
【解析】【解析】
△ABC是等边三角形，由折叠可知，AD＝BD＝0.5AB＝0.5a，易得△ADE是等边三角形．故周长是1.5a。故选 C． 如图，下图是汽车行驶速度（千米/时）和时间（分）的关系图，下列说法其中正确的个数为（ ）
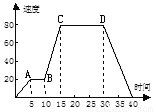
（1）汽车行驶时间为40分钟；（2）AB表示汽车匀速行驶；（3）在第30分钟时，汽车的速度是90千米/时；（4）第40分钟时，汽车停下来了.
A. 1个 B. 2个 C. 3个 D. 4个
C
【解析】试题分析：仔细分析图象特征，根据横轴和纵轴的意义依次分析各小题即可作出判断.
【解析】
由图可得，在x=40时，速度为0，故（1）（3）正确；
AB段，y的值相等，故速度不变，故（2）正确；
x=30时，y=80，即在第30分钟时，汽车的速度是80千米/时；故（4）错误；
故选C． 在△ABC中，∠C＝90°，a＝5，c＝17，用科学计算器求∠A约等于 ( )
A. 17.6° B. 17°6′ C. 17°16′ D. 17.16°
A
【解析】试题解析：sinA=，
A=sin-10.294=17.6°，
故选A． 直角坐标系中，已知点P(－2，－1)，点T(t，0)是x轴上的一个动点.
(1)求点P关于原点的对称点P′的坐标;
(2)当t取何值时，△P′TO是等腰三角形?
（1）点P关于原点的对称点P′的坐标为(2，1)；（2）综上所述，符合条件的t的值为－， ， ，4.
【解析】试题分析: （1）根据坐标关于原点对称的特点即可得出点P′的坐标,（2）要分类讨论,动点T在原点左侧和右侧时分别进行讨论即可得出当t取何值时,△P′TO是等腰三角形.
试题解析:(1) 点P关于原点的对称点P′的坐标为(2,1).
(2)OP′=.
(a)动点T在原... 将点A(3，2)沿x轴向左平移4个单位长度得到点A′，则点A′关于原点对称的点的坐标是( )
A. (-3，2) B. (-1，2) C. (1，2) D. (1，-2)
D
【解析】试题分析：将点A（3，2）向左平移4个单位长度得点A′，可得点A′的坐标为（﹣1，2），所以点A′关于y轴对称的点的坐标是（1，2），故选D． 如图，在△ABC中，∠ACB=90°，CD是AB边上的高，AB=13cm，BC=12cm，AC=5cm，求：(1)△ABC的面积；(2)CD的长．
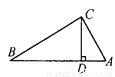
(1)30cm2;(2) cm.
【解析】（1）根据直角三角形面积的求法，即可得出△ABC的面积，
（2）根据三角形的面积公式即可求得CD的长，
【解析】
（1）∵∠ACB=90°，BC=12cm，AC=5cm，
∴S△ABC=BC×AC=30cm2，
（2）∵S△ABC=AB×CD=30cm2，
∴CD=30÷AB=cm， 五条线段的长分别为1，2，3，4，5，以其中任意三条线段为边长可以________个三角形．
3
【解析】试题解析：由三角形的两边之和大于第三边,两边之差小于第三边可知
在所给数组中能组成三角形的是2、3、4;2、4、5和3、4、5三组.
故答案为：3. 如图，已知tan O＝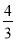
，点P在边OA上，OP＝5，点M，N在边OB上，PM＝PN，如果MN＝2，那么PM＝________．
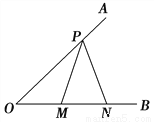
【解析】试题解析：过P作PD⊥OB，交OB于点D，
∴设PD=4x，则OD=3x，
∵OP=5,由勾股定理得：
∴x=1，
∴PD=4，
∵PM=PN，PD⊥OB，MN=2
在Rt△PMD中，由勾股定理得：
故答案为：