题目内容
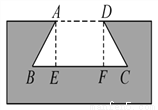
如图，工作人员在一块长方体的铁块中挖掉了一部分，留下一个燕尾槽，上口宽AD为180mm，下口宽BC为278mm，槽深为70mm.求它的燕尾角．(精确到1°)
55°
【解析】试题分析：过A作AE⊥BC与点E，则BC=AD+2BE，可求得BE的长，在直角中，根据三角函数，从而求解．
试题解析：作AE⊥BC于E，DF⊥BC于F，
所以
在中，
答：它的燕尾角为
练习册系列答案
相关题目
下列计算正确的是( )
A. -bx2y3÷2xy3=-3x B. (-xy2)2÷(-x2y)=-y3
C. (-2x2y2)3÷(-xy)3=-2x3y3 D. -(-a3b2)÷(-a2b2)=a4
B
【解析】选项A，-bx2y3÷2xy3=-bx;选项B，原式==-y3；选项C，(-2x2y2)3÷(-xy)3=8x3y3;选项D，-(-a3b2)÷(-a2b2)=-a.故选B. 两条直线平行，同旁内角相等。 （___）
×
【解析】试题分析：两条平行线被第三条直线所截，所形成的同旁内角互补，故本题的答案为“×”． 如图，下图是汽车行驶速度（千米/时）和时间（分）的关系图，下列说法其中正确的个数为（ ）
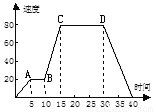
（1）汽车行驶时间为40分钟；（2）AB表示汽车匀速行驶；（3）在第30分钟时，汽车的速度是90千米/时；（4）第40分钟时，汽车停下来了.
A. 1个 B. 2个 C. 3个 D. 4个
C
【解析】试题分析：仔细分析图象特征，根据横轴和纵轴的意义依次分析各小题即可作出判断.
【解析】
由图可得，在x=40时，速度为0，故（1）（3）正确；
AB段，y的值相等，故速度不变，故（2）正确；
x=30时，y=80，即在第30分钟时，汽车的速度是80千米/时；故（4）错误；
故选C． 被誉为“沙漠之舟”的骆驼，其体温随着气温的变化而变化．在这个问题中，自变量是（ ）
A. 骆驼 B. 沙漠 C. 气温 D. 体温
C
【解析】由于体温随着气温的变化而变化，则自变量是气温，因变量是体温．
故选：C. 在△ABC中，∠C＝90°，a＝5，c＝17，用科学计算器求∠A约等于 ( )
A. 17.6° B. 17°6′ C. 17°16′ D. 17.16°
A
【解析】试题解析：sinA=，
A=sin-10.294=17.6°，
故选A． 直角坐标系中，已知点P(－2，－1)，点T(t，0)是x轴上的一个动点.
(1)求点P关于原点的对称点P′的坐标;
(2)当t取何值时，△P′TO是等腰三角形?
（1）点P关于原点的对称点P′的坐标为(2，1)；（2）综上所述，符合条件的t的值为－， ， ，4.
【解析】试题分析: （1）根据坐标关于原点对称的特点即可得出点P′的坐标,（2）要分类讨论,动点T在原点左侧和右侧时分别进行讨论即可得出当t取何值时,△P′TO是等腰三角形.
试题解析:(1) 点P关于原点的对称点P′的坐标为(2,1).
(2)OP′=.
(a)动点T在原... 如图，在△ABC中，∠ACB=90°，CD是AB边上的高，AB=13cm，BC=12cm，AC=5cm，求：(1)△ABC的面积；(2)CD的长．
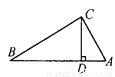
(1)30cm2;(2) cm.
【解析】（1）根据直角三角形面积的求法，即可得出△ABC的面积，
（2）根据三角形的面积公式即可求得CD的长，
【解析】
（1）∵∠ACB=90°，BC=12cm，AC=5cm，
∴S△ABC=BC×AC=30cm2，
（2）∵S△ABC=AB×CD=30cm2，
∴CD=30÷AB=cm， 如图,已知△ABC和△BDE均为等边三角形.试说明:BD+CD=AD.
见解析
【解析】首先证明△ABE≌△CBD，进而得到DC=AE，再由AD=AE+ED利用等量代换即可证出AD=BD+CD．
证明：因为△ABC,△BDE均为等边三角形,
所以BE=BD=DE,AB=BC,∠ABC=∠EBD=60°.
所以∠ABE+∠EBC=∠DBC+∠EBC.
所以∠ABE=∠DBC.
在△ABE和△CBD中,
所以△ABE≌△CBD(S...