题目内容
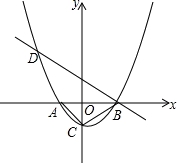
如图,已知抛物线y=m(x+1)(x﹣2)(m为常数,且m>0)与x轴从左至右依次交于A、B两点,与y轴交于点C,且OA=OC,经过点B的直线与抛物线的另一交点D在第二象限.
(1)求抛物线的函数表达式.
(2)在第一象限内的抛物线上是否存在点P,使得以A、B、P为顶点的三角形与△ABC相似?若存在,求出点P的坐标;若不存在,请说明理由.
(3)若∠DBA=30°,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?
【考点】二次函数综合题.
【分析】(1)首先求出点A、B坐标,然后根据OA=OC,求得点D坐标,代入抛物线y=m(x+1)(x﹣2)(m为常数,且m>0),求得抛物线解析式;
(2)因为点P在第一象限内的抛物线上,所以∠ABP为钝角.因此若两个三角形相似,只可能是△ABC∽△APB或△ABC∽△PAB.如答图2,按照以上两种情况进行分类讨论,分别计算;
(3)由题意,动点M运动的路径为折线AF+DF,运动时间:t=AF+ DF.如答图3,作辅助线,将AF+
DF.如答图3,作辅助线,将AF+ DF转化为AF+FG;再由垂线段最短,得到垂线段AH与直线BD的交点,即为所求的F点.
DF转化为AF+FG;再由垂线段最短,得到垂线段AH与直线BD的交点,即为所求的F点.
【解答】解:(1)抛物线y=m(x+1)(x﹣2)(m为常数,且m>0)与x轴从左至右依次交于A、B两点,
令y=0,解得x=﹣1或x=2,
则A(﹣1,0),B(2,0),
∵OA=OC,
∴C(0,﹣1),
 ∵点C(0,﹣1)在抛物线y=m(x+1)(x﹣2)上,
∵点C(0,﹣1)在抛物线y=m(x+1)(x﹣2)上,
∴m×(0+1)×(0﹣2)=﹣1,
解得m= .
.
∴抛物线的函数表达式为:y= (x+1)(x﹣2).
(x+1)(x﹣2).
(2)因为点P在第一象限内的抛物线上,所以∠ABP为钝角.
因此若两个三角形相似,只可能是△ABC∽△APB或△ABC∽△PAB.

①若△ABC∽△APB,则有∠BAC=∠PAB,如答图2﹣1所示.
设P(m,n),过点P作PN⊥x轴于点N,则ON=m,PN=n.
tan∠BAC=tan∠PAB,即:n=m+1,
∴P(m,m+1),代入抛物线解析式y= (x+1)(x﹣2),
(x+1)(x﹣2),
得 (m+1)(m﹣2)=m+1,
(m+1)(m﹣2)=m+1,
解得:m=4或m=﹣1(与点A重合,舍去),
∴P(4,5).
②若△ABC∽△PAB,则有∠ABC=∠PAB,如答图2﹣2所示.
设P(m,n),过点P作PN⊥x轴于点N,则ON=m,PN=n.
tan∠ABC=tan∠PAB,即: =
= ,n=
,n= (m+1),
(m+1),
∴P[m, (m+1)],代入抛物线解析式y=
(m+1)],代入抛物线解析式y= (x+1)(x﹣2),
(x+1)(x﹣2),
得 (m+1)(m﹣2)=
(m+1)(m﹣2)= (m+1),
(m+1),
解得:m=3或m=﹣1(与点A重合,舍去),
∴P(3,2).
故点P的坐标为(4,5)或(3,2);
(3)∵∠DBA=30°,
∴设直线BD的解析式为y=﹣ x+b,
x+b,
∵B(2,0),
∴0=﹣ ×2+b,解得b=
×2+b,解得b= .
.
故直线BD的解析式为y=﹣ x+
x+ .
.
联立两解析式可得 ,
,
解得 ,
, .
.
则D(﹣ ,
, ),
),
如答图3,过点D作DN⊥x轴于点N,过点D作DK∥x轴,则∠KDF=∠DBA=30°.过点F作FG⊥DK于点G,则FG= DF.
DF.

由题意,动点M运动的路径为折线AF+DF,运动时间:t=AF+ DF,
DF,
∴t=AF+FG,即运动的时间值等于折线AF+FG的长度值.
由垂线段最短可知,折线AF+FG的长度的最小值为DK与x轴之间的垂线段.
过点A作AH⊥DK于点H,则t最小=AH,AH与直线BD的交点,即为所求的F点.
∵A点横坐标为﹣1,直线BD解析式为:y=﹣ x+
x+ ,
,
∴y=﹣ ×(﹣1)+
×(﹣1)+ =
= ,
,
∴F(﹣1, ).
).
综上所述,当点F坐标为(﹣1, )时,点M在整个运动过程中用时最少.
)时,点M在整个运动过程中用时最少.
【点评】本题是二次函数压轴题,难度很大.第(2)问中需要分类讨论,避免漏解;在计算过程中,解析式中含有未知数m,增加了计算的难度,注意解题过程中的技巧;第(3)问中,运用了转化思想使得试题难度大大降低,需要认真体会.

 ;
;  B和点C分别以每秒3个
B和点C分别以每秒3个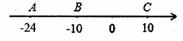
 =__________.
=__________.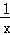 ,(4)y=2﹣1﹣3x,(5)y=x2﹣1.
,(4)y=2﹣1﹣3x,(5)y=x2﹣1.