题目内容
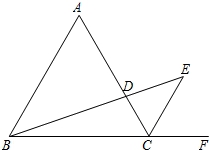
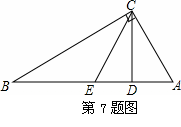
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连接BD并延长交CE于点E,若AB=6,AD=2CD,则BE的长为__________.
3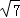 .
.
【考点】相似三角形的判定与性质;等边三角形的性质;勾股定理.
【分析】如图,作辅助线;证明AB∥CF,得到△ABD∽△CED,进而得到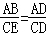 ,结合AD=2CD,AB=6,求出CE=3;求出EG、CG的长度,运用勾股定理即可解决问题.
,结合AD=2CD,AB=6,求出CE=3;求出EG、CG的长度,运用勾股定理即可解决问题.
【解答】解:如图,过点E作EG⊥CF于点G;
∵△ABC是 等边三角形,
等边三角形,
∴∠A=∠ACB=60°,AB=BC=6;
∴∠ACF=120°,而CE是外角平分线,
∴∠ACE=∠ECG=60°,∠A=∠ACE,
∴AB∥CF,△ABD∽△CED,
∴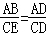 ,而AD=2CD,AB=6,
,而AD=2CD,AB=6,
∴CE=3;而∠ECG=60°,
∴∠CEG=30°,CG=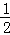 CE=1.5,EG=
CE=1.5,EG=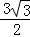 ,
,
∴BG=7.5;
由勾股定理得:BE2=BG2+EG2,
∴BE=3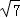 ,
,
故答案为3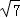 .
.

【点评】该题主要考查了等边三角形的性质、相似三角形的判定、勾股定理等几何知识点及其应用问题;解题的关键是作辅助线;灵活运用等边三角形的性质、相似三角形的判定、勾股定理等几何知识点来分析、判断、解答.

练习册系列答案
相关题目
 始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”,如:小明在编号为3的点,那么他应走3段弧长,即从3→4→5→1力第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.若小明从编号为4的点开始,第2015次“移位”后,他到达编号为 的点.
始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”,如:小明在编号为3的点,那么他应走3段弧长,即从3→4→5→1力第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.若小明从编号为4的点开始,第2015次“移位”后,他到达编号为 的点.
 <2
<2
 ﹣3
﹣3 ﹣
﹣ ×
× .
.
 ﹣3×(﹣2)2
﹣3×(﹣2)2 B.
B. C.
C. D.
D.