题目内容
如图，△ABC中，AE交BC于点D，∠C=∠E，AD：DE=3：5，AE=8，BD=4，求DC的长．考点：相似三角形的判定与性质
专题：
分析：根据相似三角形的判定与性质，可得
=
，再根据AD：DE=3：5，AE=8，可得AD、DE的长，根据比例的性质，可得答案．
| DC |
| DE |
| AD |
| BD |
解答：
解：∵∠C=∠E，∠ADC=∠BDE，
∴△ADC∽△BDE，
∴
=
，
又∵AD：DE=3：5，AE=8，
∴AD=3，DE=5，
∵BD=4，
∴
=
，即
=
．
∴DC=
．
解：∵∠C=∠E，∠ADC=∠BDE，∴△ADC∽△BDE，
∴
| DC |
| DE |
| AD |
| BD |
又∵AD：DE=3：5，AE=8，
∴AD=3，DE=5，
∵BD=4，
∴
| DC |
| DE |
| AD |
| BD |
| DC |
| 5 |
| 3 |
| 4 |
∴DC=
| 15 |
| 4 |
点评：本题考查了相似三角形的判定与性质，利用了相似三角形的判定与性质，比例的性质．
练习册系列答案
阅读快车系列答案
相关题目
若分式
有意义，则x应满足的条件为（ ）
| 1 |
| x-1 |
| A、x≠-1 | B、x≠1 |
| C、x=±1 | D、x≠±1 |
根据全国第六次人口普查统计，温州市常住人口约为9650000人，近似数9650000用科学记数法可表示为（ ）
| A、9.65×104 |
| B、9.65×105 |
| C、9.65×106 |
| D、9.65×107 |
如图，平行四边形ABCD中，E为DC的中点，AC与BE交于点F．则△EFC与△BFA的面积比为（ ）A、1：
| ||
| B、1：2 | ||
| C、1：4 | ||
| D、1：8 |
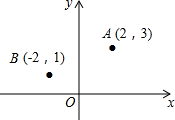如图，在平面直角坐标系中，点A，B的坐标分别为（2，3），（2，1）．
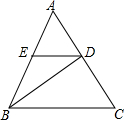已知：如图，BD是等腰三角形ABC的底边AC上的高，∠ADE=∠C．求证：△BDE是等腰三角形．
如图，Rt△ABC中，∠C=90°，有三个正方形CDEF、DGHK、GRPQ，它们分别是△ACB、△EDB和△HGB的内接正方形，EF=8cm，HK=6cm，则第三个正方形的边长PQ的长为（ ）| A、4cm | B、5cm |
| C、4.5cm | D、4.9cm |
