题目内容
 如图,Rt△ABC中,∠C=90°,有三个正方形CDEF、DGHK、GRPQ,它们分别是△ACB、△EDB和△HGB的内接正方形,EF=8cm,HK=6cm,则第三个正方形的边长PQ的长为( )
如图,Rt△ABC中,∠C=90°,有三个正方形CDEF、DGHK、GRPQ,它们分别是△ACB、△EDB和△HGB的内接正方形,EF=8cm,HK=6cm,则第三个正方形的边长PQ的长为( )| A、4cm | B、5cm |
| C、4.5cm | D、4.9cm |
考点:相似三角形的判定与性质,正方形的性质
专题:
分析:根据正方形的性质可求得EK=DE-DK=2,设PQ=x,可表示出HQ,再结合条件可证得△EKH∽△HQP,可求得x的值,可得出答案.
解答:解:
∵四边形CDEF、DGHK、GRPQ均为正方形,
∴DE=EF=8cm,HK=DK=6cm,PQ=QG,∠EKH=∠HQP=90°,
设PQ=xcm,则QG=xcm,
∴HQ=HG-GQ=(6-x)cm,
且ED∥HG,
∴∠HEK=∠PHQ,
∴△EKH∽△HQP,
∴
=
,即
=
,
解得x=4.5,
∴PQ的长为4.5cm,
故选C.
∵四边形CDEF、DGHK、GRPQ均为正方形,
∴DE=EF=8cm,HK=DK=6cm,PQ=QG,∠EKH=∠HQP=90°,
设PQ=xcm,则QG=xcm,
∴HQ=HG-GQ=(6-x)cm,
且ED∥HG,
∴∠HEK=∠PHQ,
∴△EKH∽△HQP,
∴
| EK |
| HQ |
| HK |
| PQ |
| 2 |
| 6-x |
| 6 |
| x |
解得x=4.5,
∴PQ的长为4.5cm,
故选C.
点评:本题主要考查正方形的性质及相似三角形的判定和性质,掌握正方形的四边相等、相似三角形的对应边成比例是解题的关键,注意方程思想的应用.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 如图,二次函数y=ax2+bx的图象经过原点,顶点的纵坐标为2,若一元二次方程
如图,二次函数y=ax2+bx的图象经过原点,顶点的纵坐标为2,若一元二次方程ax2+bx+k=0有实数根,则k的取值范围是( )
| A、k≤-2 | B、k≥2 |
| C、k≤2 | D、k≥-2 |
 如图,△ABC中,AE交BC于点D,∠C=∠E,AD:DE=3:5,AE=8,BD=4,求DC的长.
如图,△ABC中,AE交BC于点D,∠C=∠E,AD:DE=3:5,AE=8,BD=4,求DC的长. 如图,直角梯形ABCD,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边△ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
如图,直角梯形ABCD,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边△ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.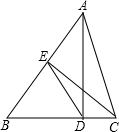 如图,在△ABC中,AD⊥BC,CE⊥AB,D,E为垂足,联结DE.
如图,在△ABC中,AD⊥BC,CE⊥AB,D,E为垂足,联结DE. 如图,直线y=
如图,直线y= 每个小正方形边长均为1,求四边形ABCD的边长和面积.
每个小正方形边长均为1,求四边形ABCD的边长和面积.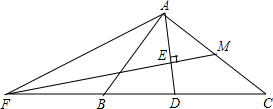 如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线EF交CB的延长线于点F,交AD于点E,交AC于点M.
如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线EF交CB的延长线于点F,交AD于点E,交AC于点M.