题目内容
12.为更好的落实阳光体育运动,学校需要购买一批足球和篮球,已知一个足球比一个篮球的单价高20元,买一个足球和两个篮球一共需要260元.(1)求足球和篮球的单价;
(2)学校决定购买足球和篮球共50个,为了加大校园足球活动开展力度,现要求用于购买这批足球和篮球的资金不超过4600元,且购买的足球尽可能多,那么学校该买多少个足球?
分析 (1)设足球的单价为x元/个,篮球的单价为y元/个,根据“一个足球比一个篮球的单价高20元,买一个足球和两个篮球一共需要260元”,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设购买足球m个,则购买篮球(50-m)个,根据总价=单价×数量结合总资金不超过4600元,即可得出关于m的一元一次不等式,解之即可得出m的取值范围,取其内的最大值即可.
解答 解:(1)设足球的单价为x元/个,篮球的单价为y元/个,
根据题意得:$\left\{\begin{array}{l}{x-y=20}\\{x+2y=260}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=100}\\{y=80}\end{array}\right.$.
答:足球的单价为100元/个,篮球的单价为80元/个.
(2)设购买足球m个,则购买篮球(50-m)个,
根据题意得:100m+80(50-m)≤4600,
解得:m≤30.
答:学校该买30个足球.
点评 本题考查了一元一次不等式的应用以及二元一次方程组的应用,解题的关键是:(1)找准等量关系,列出关于x、y的二元一次方程组;(2)根据总价=单价×数量,列出关于m的一元一次不等式.

练习册系列答案
相关题目
1. 如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=60°,则∠1等于( )
如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=60°,则∠1等于( )
 如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=60°,则∠1等于( )
如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=60°,则∠1等于( )| A. | 120° | B. | 110° | C. | 100° | D. | 80° |
 如图,∠1=∠2,D为BC的中点,求证:AB=AC.
如图,∠1=∠2,D为BC的中点,求证:AB=AC.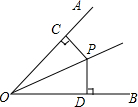 如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,求证:CP=DP.
如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,求证:CP=DP.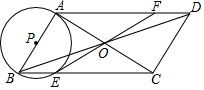 如图,在四边形ABCD中,对角线AC,BD相交于点O,且OA=OC,OB=OD,∠BAC=90°,以AB为直径的⊙P交BC于点E,连接EO并延长交AD于点F.
如图,在四边形ABCD中,对角线AC,BD相交于点O,且OA=OC,OB=OD,∠BAC=90°,以AB为直径的⊙P交BC于点E,连接EO并延长交AD于点F.