题目内容
4.在关于x、y的二元一次方程组$\left\{\begin{array}{l}{x-y=2m+1①}\\{x+2y=3m②}\end{array}\right.$中,已知x>1,y<2.求m的取值范围.分析 首先根据二元一次方程组的求解方法,求出关于x、y的二元一次方程组$\left\{\begin{array}{l}{x-y=2m+1①}\\{x+2y=3m②}\end{array}\right.$的解是多少;然后根据x>1,y<2,求出m的取值范围是多少即可.
解答 解:①×2+②,可得
3x=7m+2,
解得x=$\frac{7m+2}{3}$,
把x=$\frac{7m+2}{3}$代入①,可得
y=$\frac{m-1}{3}$,
∵x>1,y<2,
∴$\left\{\begin{array}{l}{\frac{7m+2}{3}>1}\\{\frac{m-1}{3}<2}\end{array}\right.$,
解得:$\frac{1}{7}$<m<7.
答:m的取值范围是$\frac{1}{7}$<m<7.
点评 此题主要考查了二元一次方程组的解,以及一元一次不等式组的求解方法,熟练掌握运算法则是解题的关键.

练习册系列答案
相关题目
20. 济南大明湖畔的“超然楼”被称作“江北第一楼”,某校数学社团的同学对超然楼的高度进行了测量,如图,他们在A处仰望塔顶,测得仰角为30°,再往楼的方向前进60m至B处,测得仰角为60°,若学生的身高忽略不计,$\sqrt{3}$≈1.7,结果精确到1m,则该楼的高度CD为( )
济南大明湖畔的“超然楼”被称作“江北第一楼”,某校数学社团的同学对超然楼的高度进行了测量,如图,他们在A处仰望塔顶,测得仰角为30°,再往楼的方向前进60m至B处,测得仰角为60°,若学生的身高忽略不计,$\sqrt{3}$≈1.7,结果精确到1m,则该楼的高度CD为( )
 济南大明湖畔的“超然楼”被称作“江北第一楼”,某校数学社团的同学对超然楼的高度进行了测量,如图,他们在A处仰望塔顶,测得仰角为30°,再往楼的方向前进60m至B处,测得仰角为60°,若学生的身高忽略不计,$\sqrt{3}$≈1.7,结果精确到1m,则该楼的高度CD为( )
济南大明湖畔的“超然楼”被称作“江北第一楼”,某校数学社团的同学对超然楼的高度进行了测量,如图,他们在A处仰望塔顶,测得仰角为30°,再往楼的方向前进60m至B处,测得仰角为60°,若学生的身高忽略不计,$\sqrt{3}$≈1.7,结果精确到1m,则该楼的高度CD为( )| A. | 47m | B. | 51m | C. | 53m | D. | 54m |
12.某批发商以每件50元的价格购进800件T恤.第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓时单价为40元.设第二个月单价降低x元.
(1)填表(不需化简):
(2)如果销售这批T恤获得的利润用W元表示,求W与x之间的函数关系式;
(3)如果批发商希望销售这批T恤的利润不低于8000元,那么第二个月的降价幅度应在什么范围内?
(1)填表(不需化简):
| 时 间 | 第一个月 | 第二个月 | 清仓时 |
| 单 价(元) | 80 | 40 | |
| 销售量(件) | 200 |
(3)如果批发商希望销售这批T恤的利润不低于8000元,那么第二个月的降价幅度应在什么范围内?
9.下列计算中,正确的是( )
| A. | 2a2+3a2=5a2 | B. | (a-b)2=a2-b2 | C. | a3•a2=a6 | D. | (-2a3)2=8a6 |
16.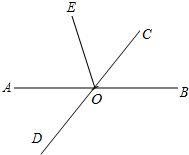 如图,已知直线AB与CD相交于点O,OC平分∠BOE,若∠AOE=80°,则∠AOD的度数为( )
如图,已知直线AB与CD相交于点O,OC平分∠BOE,若∠AOE=80°,则∠AOD的度数为( )
 如图,已知直线AB与CD相交于点O,OC平分∠BOE,若∠AOE=80°,则∠AOD的度数为( )
如图,已知直线AB与CD相交于点O,OC平分∠BOE,若∠AOE=80°,则∠AOD的度数为( )| A. | 80° | B. | 70° | C. | 60° | D. | 50° |
14.方程5x+2y=-9与下列方程构成的方程组的解为$\left\{\begin{array}{l}{x=-2}\\{y=\frac{1}{2}}\end{array}\right.$的是( )
| A. | x+2y=1 | B. | 5x+4y=-3 | C. | 3x-4y=-8 | D. | 3x+2y=-8 |
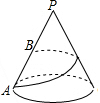 已知圆锥底面半径为1,母线长为4,地面圆周上有一点A,一只蚂蚁从点A出发沿圆锥侧面运动一周后到达母线PA中点B,则蚂蚁爬行的最短路程为2$\sqrt{5}$(结果保留根号)
已知圆锥底面半径为1,母线长为4,地面圆周上有一点A,一只蚂蚁从点A出发沿圆锥侧面运动一周后到达母线PA中点B,则蚂蚁爬行的最短路程为2$\sqrt{5}$(结果保留根号)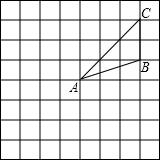 如图所示,在边长为1的网格中,△ABC绕点A按逆时针方向旋转90°,再向下平移2格后的图形△A′B′C′.
如图所示,在边长为1的网格中,△ABC绕点A按逆时针方向旋转90°,再向下平移2格后的图形△A′B′C′.