题目内容
17.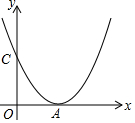 二次函数y=$\frac{1}{2}$(x+h)2的图象如图所示,已知OA=OC,试求该抛物线的解析式.
二次函数y=$\frac{1}{2}$(x+h)2的图象如图所示,已知OA=OC,试求该抛物线的解析式.
分析 先根据坐标轴上点的坐标特征用h表示A点和C点坐标得A(-h,0),C(0,$\frac{1}{2}$h2),再利用OA=OC得到-h=$\frac{1}{2}$h2,解关于h的方程求出h即可得到抛物线的解析式.
解答 解:∵y=$\frac{1}{2}$(x+h)2,
∴当x=0时,y=$\frac{1}{2}$h2,则C(0,$\frac{1}{2}$h2),
当y=0时,$\frac{1}{2}$(x+h)2=0,解得x=-h,则A(-h,0),
∵OA=OC,
∴-h=$\frac{1}{2}$h2,解得h=0(舍去)或h=-2,
∴抛物线解析式为y=$\frac{1}{2}$(x-2)2.
点评 本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
12.下列各式中的大小关系成立的是( )
| A. | $-0.3<-\frac{1}{3}$ | B. | $-\frac{6}{5}>-\frac{7}{6}$ | C. | (-2)3>(-2)2 | D. | $-\frac{9}{10}>-\frac{10}{9}$ |
20.绝对值大于2且不大于5的所有的整数的和是( )
| A. | 7 | B. | -7 | C. | 0 | D. | 5 |
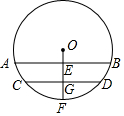 如图,圆柱形水管内原有积水的水平面宽CD=10cm,水深GF=1cm,若水面上升1cm(EG=1cm),则此时水面宽AB为多少?
如图,圆柱形水管内原有积水的水平面宽CD=10cm,水深GF=1cm,若水面上升1cm(EG=1cm),则此时水面宽AB为多少?
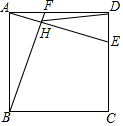 如图,在边长为2的正方形ABCD中,点E在边DC上运动,点F在边AD上运动,且DE=AF,AE,BF交于点H,连接DH,则DH的最小值为$\sqrt{5}-1$.
如图,在边长为2的正方形ABCD中,点E在边DC上运动,点F在边AD上运动,且DE=AF,AE,BF交于点H,连接DH,则DH的最小值为$\sqrt{5}-1$.