题目内容
14.已知四组数据:①1.5,2,2.5;②3,4,5;③40,50,60;④$\frac{5}{4}$,1,$\frac{3}{4}$.分别以每组数据中的三个数为三角形的三边长,构成直角三角形的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据勾股定理的逆定理,只要两边的平方和等于第三边的平方即可构成直角三角形.只要判断两个较小的数的平方和是否等于最大数的平方即可判断.
解答 解:①∵1.52+22=2.52,
∴以这三个数为长度的线段能构成直角三角形;
②∵32+42=52,
∴以这三个数为长度的线段能构成直角三角形;
③∵402+502≠602 ,
∴以这三个数为长度的线段不能构成直角三角形;
③∵$\frac{3}{4}$2+12=$\frac{5}{4}$2 ,
∴以这三个数为长度的线段能构成直角三角形;
故选:C.
点评 本题主要考查了勾股定理的逆定理,已知三条线段的长,判断是否能构成直角三角形的三边,判断的方法是:判断两个较小的数的平方和是否等于最大数的平方即可判断.

练习册系列答案
相关题目
19.数字$\sqrt{2}$、$\frac{1}{3}$,π,$\root{3}{8}$,0.$\stackrel{•}{3}\stackrel{•}{2}$中无理数的个数有多少个( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
6.下列计算正确的是( )
| A. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{2}$ | B. | a8÷a4=a2 | C. | (a-b)2=a2-b2 | D. | 3m+4n=7mn |
3.已知三角形的两边长分别为8和4,则第三边长可能是( )
| A. | 3 | B. | 4 | C. | 8 | D. | 12 |
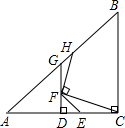 如图,CE=GF,AC=BC,∠ACB=90°,D是中点,DG⊥AC,FH⊥FC.
如图,CE=GF,AC=BC,∠ACB=90°,D是中点,DG⊥AC,FH⊥FC.
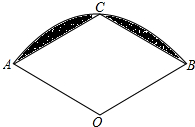 如图,扇形AOB,半径OA=2,∠AOB=120°,C是弧AB的中点,连AC、BC,求图中阴影部分的面积.
如图,扇形AOB,半径OA=2,∠AOB=120°,C是弧AB的中点,连AC、BC,求图中阴影部分的面积.