题目内容
 如图,反比例函数y=
如图,反比例函数y=| k |
| x |
(1)求反比例函数与一次函数的解析式.
(2)根据图象回答:当x取何值时,反比例函数的值大于一次函数的值?
考点:反比例函数与一次函数的交点问题
专题:待定系数法
分析:(1)把A的坐标代入反比例函数的解析式即可求出解析式,求出B的坐标,把A、B的坐标代入一次函数解析式得出方程组,求出方程组的解,即可得出一次函数的解析式;
(2)根据图象和A、B坐标得出即可.
(2)根据图象和A、B坐标得出即可.
解答:解:(1)∵把A(-1,4)代入y=
中,
得k=-4,
∴反比例函数的解析式是:y=-
,
∵把B(n,-2)代入y=-
得:-2=-
,
∴n=2
把A(-1,4),B(2,-2)代入y=mx+b中,
得
,
解得:
∴一次函数的解析式是:y=-2x+2;
(2)由图象可知,当-1<x<0或x>2时,
反比例函数的值大于一次函数的值.
| k |
| x |
得k=-4,
∴反比例函数的解析式是:y=-
| 4 |
| x |
∵把B(n,-2)代入y=-
| 4 |
| x |
得:-2=-
| 4 |
| n |
∴n=2
把A(-1,4),B(2,-2)代入y=mx+b中,
得
|
解得:
|
∴一次函数的解析式是:y=-2x+2;
(2)由图象可知,当-1<x<0或x>2时,
反比例函数的值大于一次函数的值.
点评:本题考查了用待定系数法求反比例函数、一次函数的解析式,一次函数和反比例函数的交点问题的应用,主要考查学生的计算能力,用了数形结合思想.

练习册系列答案
相关题目
某中学八年级一班5名同学某一周踢足球的时间为别为5小时,4小时,3小时,3小时,则数据5,4,4,3,3的方差为( )
| A、0.66 | B、0.56 |
| C、0.55 | D、0.54 |
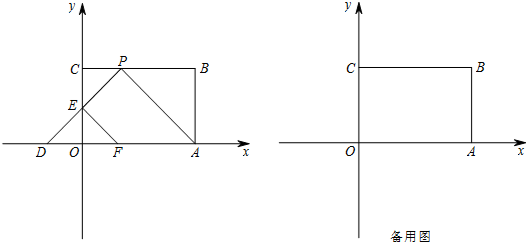
 如图,△ABC在平面直角坐标系中,三个顶点的坐标分别为A(-5,-1),B(0,4),C(0,-6).
如图,△ABC在平面直角坐标系中,三个顶点的坐标分别为A(-5,-1),B(0,4),C(0,-6).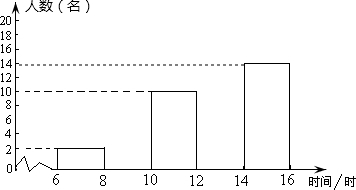 王兴喆同学为了解本校七年级500名学生“五一”放假期间参加社会实践活动的时间(单位:h),随机抽取了该年级部分学生进行了调查,并将调查结果绘制成频数分布表和频数分布直方图.请你根据图表中提供的信息,解答下列问题:
王兴喆同学为了解本校七年级500名学生“五一”放假期间参加社会实践活动的时间(单位:h),随机抽取了该年级部分学生进行了调查,并将调查结果绘制成频数分布表和频数分布直方图.请你根据图表中提供的信息,解答下列问题: 如图,在△ABC中,点D是BC的中点,作射线AD,在线段AD及其延长线上分别取点E、F,连接CE、BF.
如图,在△ABC中,点D是BC的中点,作射线AD,在线段AD及其延长线上分别取点E、F,连接CE、BF. 如图,梯形的上底AD=4cm,下底BC=8cm,它的一条对角线把它分成两部分,则△ABD与△BCD面积之比为
如图,梯形的上底AD=4cm,下底BC=8cm,它的一条对角线把它分成两部分,则△ABD与△BCD面积之比为