题目内容
1.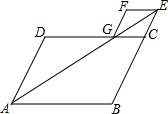 如图,在平行四边形ABCD中,∠BAD的平分线交BC的延长线于点E,交CD于点G,过点E作EF∥CD,过点G作FG∥EC,EF,FG交于点F.求证:四边形CEFG为菱形.
如图,在平行四边形ABCD中,∠BAD的平分线交BC的延长线于点E,交CD于点G,过点E作EF∥CD,过点G作FG∥EC,EF,FG交于点F.求证:四边形CEFG为菱形.
分析 首先判定四边形EFGC是平行四边形,然后得到其邻边相等证得菱形即可.
解答 证明:∵EF∥CD,FG∥EC,
∴四边形EFGC是平行四边形,
∵四边形ABCD是平行四边形,
∴∠DAE=∠BEA,∠EAB=∠EGC,
∵AG平分∠DAB,
∴∠DAG=∠BAG,
∴∠EGC=∠GEC,
∴EC=GC,
∴四边形EFGC是菱形;
点评 本题考查了菱形的判定,解题的关键是了解邻边相等的平行四边形是菱形,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.如图是中国体育代表团在近四届亚运会上获金银牌的情况.
(1)请根据表中提供的数据制成复式折线统计图.
中国体育代表团第13-16届亚运会上获得金银牌情况统计图.

(2)第16届广州亚运会上,中国代表团获得的金牌数比第14届韩国釜山获得的金牌数多百分之几?
(3)请你对我国体育代表团在第16届广州亚运会获得的成绩做简单的评价.
| 届数 | 第13届 | 第14届 | 第15届 | 第16届 |
| 金牌数(枚) | 129 | 150 | 168 | 198 |
| 银牌数(枚) | 77 | 84 | 88 | 118 |
中国体育代表团第13-16届亚运会上获得金银牌情况统计图.

(2)第16届广州亚运会上,中国代表团获得的金牌数比第14届韩国釜山获得的金牌数多百分之几?
(3)请你对我国体育代表团在第16届广州亚运会获得的成绩做简单的评价.
4.若关于x的方程x2-2(1-k)x+k2=0有实数根m和n,则m+n的取值范围是( )
| A. | m+n≥1 | B. | m+n≤1 | C. | m+n≥$\frac{1}{2}$ | D. | m+n≤$\frac{1}{2}$ |
11.下列三条线段不能构成三角形的是( )
| A. | 3,4,5 | B. | 3,3,3 | C. | 1,2,3 | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
9.如果A(1-a,b+1)在第三象限,那么点B(a,b)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
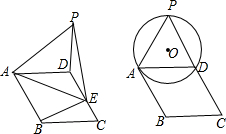 已知:如图?ABCD中,CD=CB=3,∠C=60°,点E是CD边上自C向D的动点(点E到点D停止运动),连结AE,以AE为边作等边△AEP,连结DP.
已知:如图?ABCD中,CD=CB=3,∠C=60°,点E是CD边上自C向D的动点(点E到点D停止运动),连结AE,以AE为边作等边△AEP,连结DP.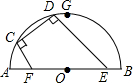 如图,AB为半圆所在⊙O的直径,弦CD为定长且小于⊙O的半径(C点与A点不重合),CF⊥CD交AB于点F,DE⊥CD交AB于点E,G为半圆弧上的中点.当点C在$\widehat{AG}$上运动时,设$\widehat{AG}$的长为x,CF+DE=y.则下列图象中,能表示y与x的函数关系的图象大致是( )
如图,AB为半圆所在⊙O的直径,弦CD为定长且小于⊙O的半径(C点与A点不重合),CF⊥CD交AB于点F,DE⊥CD交AB于点E,G为半圆弧上的中点.当点C在$\widehat{AG}$上运动时,设$\widehat{AG}$的长为x,CF+DE=y.则下列图象中,能表示y与x的函数关系的图象大致是( )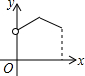

 如图所示,直线a、b被直线c所截,现给出下列四种条件:①∠3=∠7,②∠1+∠4=180°,③∠2=∠8,④∠5=∠7,其中能判断是a∥b的条件的序号是( )
如图所示,直线a、b被直线c所截,现给出下列四种条件:①∠3=∠7,②∠1+∠4=180°,③∠2=∠8,④∠5=∠7,其中能判断是a∥b的条件的序号是( )