题目内容
16.先化简,再求值:$(x-\frac{x}{x+1})÷(1+\frac{1}{{{x^2}-1}})$,其中x的值是不等式组$\left\{\begin{array}{l}2(x+1)-3>0\\-3x+2≥-4\end{array}\right.$的整数解.分析 原式括号中两项通分并利用同分母分式的加减法则计算,同时利用除法法则变形,约分得到最简结果,求出不等式组的解集,找出整数解得到x的值,代入计算即可求出值.
解答 解:原式=$\frac{x(x+1)-x}{x+1}$÷$\frac{{x}^{2}-1+1}{{x}^{2}-1}$=$\frac{{x}^{2}}{x+1}$•$\frac{(x+1)(x-1)}{{x}^{2}}$=x-1,
不等式组$\left\{\begin{array}{l}2(x+1)-3>0\\-3x+2≥-4\end{array}\right.$,
解得:$\frac{1}{2}$<x≤2,
不等式组的整数解为1,2,
当x=1时,原式没有意义,
当x=2时,原式=1.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
4.若关于x的方程x2-2(1-k)x+k2=0有实数根m和n,则m+n的取值范围是( )
| A. | m+n≥1 | B. | m+n≤1 | C. | m+n≥$\frac{1}{2}$ | D. | m+n≤$\frac{1}{2}$ |
11.下列三条线段不能构成三角形的是( )
| A. | 3,4,5 | B. | 3,3,3 | C. | 1,2,3 | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
1.以下命题中,真命题的是( )
| A. | 同位角相等 | |
| B. | 两边和一角对应相等的两个三角形全等 | |
| C. | 面积相等的两个三角形全等 | |
| D. | 等腰三角形底边中点到两腰的距离相等 |
5.下列选项中,两个角是邻补角的是( )
| A. |  | B. |  | C. |  | D. |  |

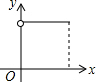
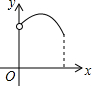
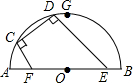 如图,AB为半圆所在⊙O的直径,弦CD为定长且小于⊙O的半径(C点与A点不重合),CF⊥CD交AB于点F,DE⊥CD交AB于点E,G为半圆弧上的中点.当点C在$\widehat{AG}$上运动时,设$\widehat{AG}$的长为x,CF+DE=y.则下列图象中,能表示y与x的函数关系的图象大致是( )
如图,AB为半圆所在⊙O的直径,弦CD为定长且小于⊙O的半径(C点与A点不重合),CF⊥CD交AB于点F,DE⊥CD交AB于点E,G为半圆弧上的中点.当点C在$\widehat{AG}$上运动时,设$\widehat{AG}$的长为x,CF+DE=y.则下列图象中,能表示y与x的函数关系的图象大致是( )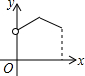

 如图所示,直线a、b被直线c所截,现给出下列四种条件:①∠3=∠7,②∠1+∠4=180°,③∠2=∠8,④∠5=∠7,其中能判断是a∥b的条件的序号是( )
如图所示,直线a、b被直线c所截,现给出下列四种条件:①∠3=∠7,②∠1+∠4=180°,③∠2=∠8,④∠5=∠7,其中能判断是a∥b的条件的序号是( )