Question

8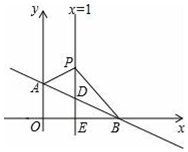． 如图，平面直角坐标系中，直线AB：交y轴于点A（0，1），交x轴于点B．直线x=1交AB于点D，交x轴于点E，P是直线x=1上一动点，且在点D的上方，设P（1，n）．
（1）求直线AB的解析式和点B的坐标；
（2）求△ABP的面积（用含n的代数式表示）．

Answer 1

分析 （1）把A的坐标代入直线AB的解析式，即可求得b的值，然后在解析式中，令y=0，求得x的值，即可求得B的坐标；
（2）过点A作AM⊥PD，垂足为M，求得AM的长，即可求得△BPD和△PAB的面积，二者的和即可求得．

解答 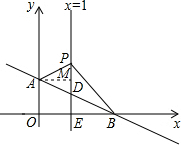解：（1）∵y=-$\frac{1}{3}$x+b经过A（0，1），
∴b=1，
∴直线AB的解析式是y=-$\frac{1}{3}$x+1．
当y=0时，0=-$\frac{1}{3}$x+1，解得x=3，
∴点B（3，0）．

（2）过点A作AM⊥PD，垂足为M，则有AM=1，
∵x=1时，y=-$\frac{1}{3}$x+1=$\frac{2}{3}$，P在点D的上方，
∴PD=n-$\frac{2}{3}$，S_△APD=$\frac{1}{2}$PD•AM=$\frac{1}{2}$（n-$\frac{2}{3}$）×1=$\frac{1}{2}$n-$\frac{1}{3}$，
由点B（3，0），可知点B到直线x=1的距离为2，即△BDP的边PD上的高长为2，
∴S_△BPD=$\frac{1}{2}$PD•BE=$\frac{1}{2}$（n-$\frac{2}{3}$）×2=n-$\frac{2}{3}$，
∴S_△ABP=S_△APD+S_△BPD=$\frac{3}{2}$n-1．

点评 本题是待定系数法求函数的解析式、一次函数图象上点的坐标特征，以及三角形的面积的综合应用，求得直线的解析式是关键．