题目内容
 如图,在正方形ABCD中,∠EAF=45°,点E、F在BD上,求证:BE2+FD2=EF2.
如图,在正方形ABCD中,∠EAF=45°,点E、F在BD上,求证:BE2+FD2=EF2.考点:旋转的性质,全等三角形的判定与性质,勾股定理,正方形的性质
专题:证明题
分析:把△ADF绕点A顺时针旋转90°得到△ABG,连接EG,根据旋转的性质可得BG=DF,AG=AF,∠BAG=∠DAF,∠ABG=∠ADF,再求出∠GAE=45°,从而得到∠GAE=∠EAF,然后利用“边角边”证明△AEG和△AEF全等,根据全等三角形对应边相等可得EF=EG,再求出∠GBE=90°,然后利用勾股定理列式证明即可.
解答: 证明:如图,把△ADF绕点A顺时针旋转90°得到△ABG,连接EG,
证明:如图,把△ADF绕点A顺时针旋转90°得到△ABG,连接EG,
∴BG=DF,AG=AF,∠BAG=∠DAF,∠ABG=∠ADF,
∵∠EAF=45°,
∴∠GAE=∠BAG+∠BAE=∠DAF+∠BAE=∠BAD-∠EAF=90°-45°=45°,
∴∠GAE=∠EAF,
在△AEG和△AEF中,
,
∴△AEG≌△AEF(SAS),
∴EF=EG,
在在正方形ABCD中,∠ABE=∠ADF=45°,
∴∠GBE=∠ABG+∠ABE=45°+45°=90°,
∴BE2+BG2=EG2,
即BE2+FD2=EF2.
 证明:如图,把△ADF绕点A顺时针旋转90°得到△ABG,连接EG,
证明:如图,把△ADF绕点A顺时针旋转90°得到△ABG,连接EG,∴BG=DF,AG=AF,∠BAG=∠DAF,∠ABG=∠ADF,
∵∠EAF=45°,
∴∠GAE=∠BAG+∠BAE=∠DAF+∠BAE=∠BAD-∠EAF=90°-45°=45°,
∴∠GAE=∠EAF,
在△AEG和△AEF中,
|
∴△AEG≌△AEF(SAS),
∴EF=EG,
在在正方形ABCD中,∠ABE=∠ADF=45°,
∴∠GBE=∠ABG+∠ABE=45°+45°=90°,
∴BE2+BG2=EG2,
即BE2+FD2=EF2.
点评:本题考查了旋转的性质,全等三角形的判定与性质,勾股定理,正方形的性质,熟记各性质是解题的关键,难点在于作辅助线构造成全等三角形和直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,抛物线y=-x2+bx+c与直线y=
如图,抛物线y=-x2+bx+c与直线y=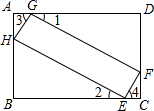 矩形ABCD中,点E,F,G,H分别在BC,CD,DA,AB上,若∠1=∠2=∠3=∠4.
矩形ABCD中,点E,F,G,H分别在BC,CD,DA,AB上,若∠1=∠2=∠3=∠4. 如图是一正方体的展开图,若正方体相对两个面上的式子的值相等,求下列代数式的值:
如图是一正方体的展开图,若正方体相对两个面上的式子的值相等,求下列代数式的值: 在边长为1的3×3的方格中,点B、O都在格点上,则劣弧BC的长是
在边长为1的3×3的方格中,点B、O都在格点上,则劣弧BC的长是