题目内容
20.先化简,再求值:$\frac{{a}^{2}-1}{{a}^{2}+2a+1}$÷$\frac{{a}^{2}-a}{a+1}$,其中a=$\sqrt{27}$-$\sqrt{12}$.分析 首先把分式的分子和分母分解因式,把除法转化为乘法,计算乘法即可化简,然后对a的值进行化简,最后代入求解即可.
解答 解:原式=$\frac{(a+1)(a-1)}{(a+1)^{2}}$•$\frac{a+1}{a(a-1)}$
=$\frac{1}{a}$.
∵a=$\sqrt{27}$-$\sqrt{12}$=3$\sqrt{3}$-2$\sqrt{3}$=$\sqrt{3}$.
∴原式=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$.
点评 本题考查了分式的化简求值以及二次根式的化简,正确把分式的分子和分母分解因式是本题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
10.下列式子中,正确的是( )
| A. | -6<-8 | B. | -$\frac{1}{5}$<-$\frac{1}{7}$ | C. | -$\frac{1}{1000}$>0 | D. | $\frac{1}{3}$<0.3 |
15. 如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D,再分别以点C、D为圆心,大于$\frac{1}{2}$CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是( )
如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D,再分别以点C、D为圆心,大于$\frac{1}{2}$CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是( )
 如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D,再分别以点C、D为圆心,大于$\frac{1}{2}$CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是( )
如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D,再分别以点C、D为圆心,大于$\frac{1}{2}$CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是( )| A. | 射线OE是∠AOB的平分线 | B. | △COD是等腰三角形 | ||
| C. | O、E两点关于CD所在直线对称 | D. | C、D两点关于OE所在直线对称 |
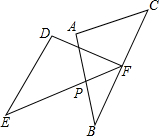 如图,△ABC≌△DEF,点F在BC边上,AB与EF相交于点P.若∠DEF=40°,PB=PF,则∠APF=80°.
如图,△ABC≌△DEF,点F在BC边上,AB与EF相交于点P.若∠DEF=40°,PB=PF,则∠APF=80°.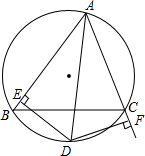 如图,△ABC中,∠A的角平分线交△ABC的外接圆于点D,DE⊥AB于E,DF⊥AC交AC的延长线于F,求证:BE=CF.
如图,△ABC中,∠A的角平分线交△ABC的外接圆于点D,DE⊥AB于E,DF⊥AC交AC的延长线于F,求证:BE=CF.