题目内容
16.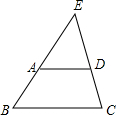 如图,在梯形ABCD中,AD∥BC.AD=3,BC=5,梯形的高线长为2.延长梯形的两条腰,相交于点E,求E到BC的距离.
如图,在梯形ABCD中,AD∥BC.AD=3,BC=5,梯形的高线长为2.延长梯形的两条腰,相交于点E,求E到BC的距离.
分析 根据AD∥BC,由相似三角形的判定证明出△ADE∽△BCE,然后根据相似三角形对应边的比等于对应边上的高的比列出比例式,将数值代入即可求解.
解答  解:过E作EH⊥BC于H,交AD于M,
解:过E作EH⊥BC于H,交AD于M,
∵AD∥BC,
∴EH⊥AD,
∵AD∥BC,
∴△EAD∽△EBC,
∴$\frac{EM}{EH}=\frac{AD}{BC}$,
∴$\frac{EH-2}{EH}=\frac{3}{5}$,
解得:EH=5,
∴E到BC的距离是5.
点评 本题主要考查了相似三角形的判定与性质,难度适中,根据△ADE∽△BCE正确地列出比例式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.以a、b、c为边,不能组成直角三角形的是( )
| A. | a=6,b=8,c=10 | B. | a=1,b=$\sqrt{3}$,c=2 | C. | a=8,b=15,c=17 | D. | a=$\frac{1}{3}$,b=$\frac{1}{4}$,c=$\frac{1}{5}$ |
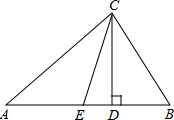 如图,在△ABC中,CD、CE分别是△ABC的高和角平分线.
如图,在△ABC中,CD、CE分别是△ABC的高和角平分线.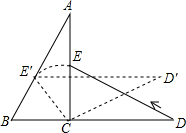 两块大小一样斜边为4且含有30°角的三角板如图5水平放置.将△CDE绕C点按逆时针方向旋转,当E点恰好落在AB上时,△CDE旋转了30°.
两块大小一样斜边为4且含有30°角的三角板如图5水平放置.将△CDE绕C点按逆时针方向旋转,当E点恰好落在AB上时,△CDE旋转了30°. 已知:如图,在△ABC中,∠BAC=90°,AB=AC,BD⊥DE,CE⊥ED,且DE过点A.求证:DE=BD+CE.
已知:如图,在△ABC中,∠BAC=90°,AB=AC,BD⊥DE,CE⊥ED,且DE过点A.求证:DE=BD+CE.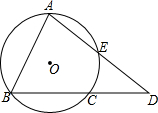 如图,A是优弧BC的中点,弦AE的延长线与BC的延长线交于D,求证:AB2=AE•AD.
如图,A是优弧BC的中点,弦AE的延长线与BC的延长线交于D,求证:AB2=AE•AD.