题目内容
4.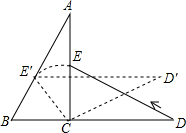 两块大小一样斜边为4且含有30°角的三角板如图5水平放置.将△CDE绕C点按逆时针方向旋转,当E点恰好落在AB上时,△CDE旋转了30°.
两块大小一样斜边为4且含有30°角的三角板如图5水平放置.将△CDE绕C点按逆时针方向旋转,当E点恰好落在AB上时,△CDE旋转了30°.
分析 根据含有30°角的直角三角形的性质可知CE′是△ACB的中线,可得△E′CB是等边三角形,从而得出∠ACE′的度数和CE′的长,从而得出△CDE旋转的度数;
解答 解:∵三角板是两块大小一样斜边为4且含有30°的角,
∴CE′是△ACB的中线,
∴CE′=BC=BE′=2,
∴△E′CB是等边三角形,
∴∠BCE′=60°,
∴∠ACE′=90°-60°=30°,
故答案为:30°.
点评 考查了含有30°角的直角三角形的性质,等边三角形的判定,旋转的性质和扇形面积的计算,本题关键是得到CE′是△ACB的中线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列图形不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
13.把二次函数y=$\frac{1}{4}{x}^{2}$+x-1化为y=a(x-h)2+k的形式是( )
| A. | y=$\frac{1}{4}$(x+1)2+2 | B. | y=$\frac{1}{4}$(x+1)2-2 | C. | y=$\frac{1}{4}$(x-2)2+2 | D. | y=$\frac{1}{4}$(x+2)2-2 |
14.某件商品现在的售价为34元.比原价降低了15%,则原来的售价是( )
| A. | 51元 | B. | 28.9元 | C. | 35元 | D. | 40元 |

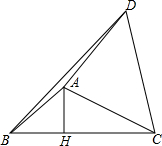 如图.在△ABC中.以AC为边在△ABC外部作等腰△ACD.使AC=AD.且∠DAC=2∠ABC,连接BD.作AH⊥BC于点H.若AH=$\frac{3}{2}$,BC=4,则BD=5.
如图.在△ABC中.以AC为边在△ABC外部作等腰△ACD.使AC=AD.且∠DAC=2∠ABC,连接BD.作AH⊥BC于点H.若AH=$\frac{3}{2}$,BC=4,则BD=5. 已知:如图,AB和CD相交于O,AO=BO,CO=DO,求证:AC=BD.
已知:如图,AB和CD相交于O,AO=BO,CO=DO,求证:AC=BD.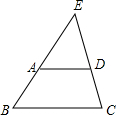 如图,在梯形ABCD中,AD∥BC.AD=3,BC=5,梯形的高线长为2.延长梯形的两条腰,相交于点E,求E到BC的距离.
如图,在梯形ABCD中,AD∥BC.AD=3,BC=5,梯形的高线长为2.延长梯形的两条腰,相交于点E,求E到BC的距离.