题目内容
5.出租车司机小李某天在出租车公司出发,如果规定以出租车公司为原点,向东为正,向西为负,上午营运时小李是在东西走向的大街上进行的,他这天上午所接六位乘客的行车里程(单位:km)如下:-2,+5,-1,+1,-6,-2,问:
(1)将最后一位乘客送到目的地时,小李在什么位置?
(2)若汽车原来有油10升,汽车耗油量为0.2L/km(升/千米),这天上午小李接送完最后一名乘客,出租车还剩余油多少升?
(3)若出租车起步价为8元,起步里程为3km(包括3km),超过部分每千米1.2元,问小李这天共得车费多少元?
分析 (1)计算出六次行车里程的和,看其结果的正负即可判断其位置;
(2)求出所记录的六次行车里程的绝对值,再计算耗油即可;
(3)不超过3km的按8元计算,超过3km的在8元的基础上,再加上超过部分乘以1.2元,即可.
解答 解:(1)-2+5-1+1-6-2=-5.
故此时小李在出车公司的西边5km的位置;
(2)|-2|+|+5|+|-1|+|+1|+|-6|+|-2|=2+5+1+1+6+2=17(千米),
10-0.2×17=6.6(L).
答:出租车共耗油6.6L;
(3)根据题意可得:6×8+(2+3)×1.2=54(元).
答:小李这天上午共得车费54元
点评 本题主要考查有理数的加减运算,注意正负数的意义,熟练掌握运算法则是解题的关键.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
13.把二次函数y=$\frac{1}{4}{x}^{2}$+x-1化为y=a(x-h)2+k的形式是( )
| A. | y=$\frac{1}{4}$(x+1)2+2 | B. | y=$\frac{1}{4}$(x+1)2-2 | C. | y=$\frac{1}{4}$(x-2)2+2 | D. | y=$\frac{1}{4}$(x+2)2-2 |
20. 把两块三角板按如图所示那样拼在一起,则∠ABC的补角等于( )
把两块三角板按如图所示那样拼在一起,则∠ABC的补角等于( )
 把两块三角板按如图所示那样拼在一起,则∠ABC的补角等于( )
把两块三角板按如图所示那样拼在一起,则∠ABC的补角等于( )| A. | 135° | B. | 60° | C. | 45° | D. | 120° |
10.下列各组单项式的和仍为单项式的是( )
| A. | 5x2y与-2xy | B. | -5x2y与πx2y | C. | 5a2y与3x2y | D. | 23与x3 |
14.某件商品现在的售价为34元.比原价降低了15%,则原来的售价是( )
| A. | 51元 | B. | 28.9元 | C. | 35元 | D. | 40元 |
15.(直接写出每小问的结果)经检测,某棵小树在1~10年间的生长高度符合一定的规律(如表):
(1)第10年,这棵小树的高度为380cm.
(2)树高h(cm)与年份n(1≤n≤10)之间的数量关系是h=180+20n〔或200+20(n-1)〕(用含n的代数式表示h).
(3)如果把树高300cm称为标准树高,记为0cm,超过标准的高度记为正数,不足标准的高度记为负数,那么第2年的树高应记为-80cm.
| 年份 | 树高(cm) |
| 1 | 200 |
| 2 | 220 |
| 3 | 240 |
| 4 | 260 |
| 5 | 280 |
| … | … |
| 10 |
(2)树高h(cm)与年份n(1≤n≤10)之间的数量关系是h=180+20n〔或200+20(n-1)〕(用含n的代数式表示h).
(3)如果把树高300cm称为标准树高,记为0cm,超过标准的高度记为正数,不足标准的高度记为负数,那么第2年的树高应记为-80cm.
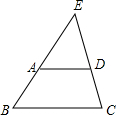 如图,在梯形ABCD中,AD∥BC.AD=3,BC=5,梯形的高线长为2.延长梯形的两条腰,相交于点E,求E到BC的距离.
如图,在梯形ABCD中,AD∥BC.AD=3,BC=5,梯形的高线长为2.延长梯形的两条腰,相交于点E,求E到BC的距离.