题目内容
7. 如图,在矩形ABCD中,两条对角线AC、BD相交于O,∠ACD=30°,AD=2.
如图,在矩形ABCD中,两条对角线AC、BD相交于O,∠ACD=30°,AD=2.(1)判断△AOD的形状;
(2)求对角线AC的长.
分析 (1)利用矩形的性质得∠ADC=90°,AO=OD=OC=OB,则∠DAC=90°-∠ACD=60°,于是可判断△AOD为等边三角形;
(2)根据等边三角形的性质得AO=AD=2,然后根据矩形的性质得AC=BD=2AO=4.
解答 解:(1)∵四边形ABCD为矩形,
∴∠ADC=90°,AO=OD=OC=OB,
∵∠ACD=30°,
∴∠DAC=90°-30°=60°,
而OA=OD,
∴△AOD为等边三角形;
(2)∵△AOD为等边三角形,
∴AO=AD=2,
∴AC=BD=2AO=4.
点评 本题考查了矩形的性质:平行四边形的性质矩形都具有;矩形的四个角都是直角;邻边垂直;矩形的对角线相等.解决本题的关键是熟练掌握等边三角形的判定与性质.

练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
9.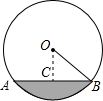 一条排水管的截面如下左图所示,已知排水管的半径OB=10,水面宽AB=16,则排水管内水的最大深度是( )
一条排水管的截面如下左图所示,已知排水管的半径OB=10,水面宽AB=16,则排水管内水的最大深度是( )
 一条排水管的截面如下左图所示,已知排水管的半径OB=10,水面宽AB=16,则排水管内水的最大深度是( )
一条排水管的截面如下左图所示,已知排水管的半径OB=10,水面宽AB=16,则排水管内水的最大深度是( )| A. | 4 | B. | 5 | C. | 6$\sqrt{3}$ | D. | 6 |
17.二次函数y=(x-1)2+1的图象顶点坐标是( )
| A. | (1,-1) | B. | (-1,1) | C. | (1,1) | D. | (-1,-1) |
 如图,平行四边形ABCD中,E、F分别为AB、AD上的点,且BE=2AE,AF=3DF,连结EF、AC,交于点G,则$\frac{AG}{CG}$的值为$\frac{3}{10}$.
如图,平行四边形ABCD中,E、F分别为AB、AD上的点,且BE=2AE,AF=3DF,连结EF、AC,交于点G,则$\frac{AG}{CG}$的值为$\frac{3}{10}$. 如图,已知等边三角形ABC边长为2,建立适当的平面直角坐标系,并写出各顶点的坐标.
如图,已知等边三角形ABC边长为2,建立适当的平面直角坐标系,并写出各顶点的坐标.
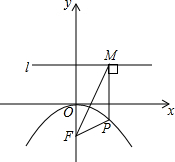 如图,抛物线的顶点是原点,抛物线经过A点(8,-8),F点坐标为(0,-2),直线l为y=2,直线l平行于x轴.P点是抛物线上任意一点,过P点作PM⊥l,垂足为M点.
如图,抛物线的顶点是原点,抛物线经过A点(8,-8),F点坐标为(0,-2),直线l为y=2,直线l平行于x轴.P点是抛物线上任意一点,过P点作PM⊥l,垂足为M点. 如图,E(-6,0),F(-4,-2),以O为位似中心按比例尺1:2把△EFO缩小到第一象限,则点F的对应点F′的坐标为(2,1).
如图,E(-6,0),F(-4,-2),以O为位似中心按比例尺1:2把△EFO缩小到第一象限,则点F的对应点F′的坐标为(2,1).