题目内容
7.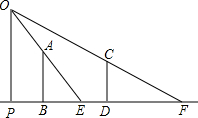 如图,路灯在马路边一电杆OP的上方,树AB、CD的影子为BE,DF,若树AB的高为12m,其影子BE的长为8m,树CD的影子DF的长为9m,∠POE+∠POF=90°,求树CD的高.
如图,路灯在马路边一电杆OP的上方,树AB、CD的影子为BE,DF,若树AB的高为12m,其影子BE的长为8m,树CD的影子DF的长为9m,∠POE+∠POF=90°,求树CD的高.
分析 根据题意得出∠BAE=∠DFC,再利用相似三角形的判定方法得出△ABE∽△FDC,进而利用相似三角形的性质得出DC的长.
解答 解:∵∠POE+∠POF=90°,∠POF+∠OFP=90°,
∴∠OPE=∠DFC,
∵OP∥AB,
∴∠POE=∠BAE,
∴∠BAE=∠DFC,
又∵∠ABE=∠CDF,
∴△ABE∽△FDC,
∴$\frac{BE}{DC}$=$\frac{AB}{DF}$,
即$\frac{8}{DC}$=$\frac{12}{9}$,
解得:DC=6,
答:树CD的高为6m.
点评 此题主要考查了相似三角形的应用,根据题意得出△ABE∽△FDC是解题关键.

练习册系列答案
相关题目
2.使分式$\frac{2-x}{(x-2){(x}^{2}-9)}$有意义的x应取( )
| A. | x≠3且x≠-3 | B. | x≠2或x≠3或x≠-3 | C. | x≠3或x≠-3 | D. | x≠2且x≠3且x≠-3 |
16.化简:(a-b)$\sqrt{-\frac{1}{a-b}}$的结果是( )
| A. | $\sqrt{a-b}$ | B. | $\sqrt{-a-b}$ | C. | -$\sqrt{a-b}$ | D. | -$\sqrt{b-a}$ |
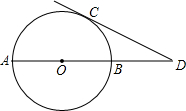 如图,AB是⊙O的直径,过点C的切线交AB的延长线于点D.若∠ADC=30°,BD=10,求⊙O的半径.
如图,AB是⊙O的直径,过点C的切线交AB的延长线于点D.若∠ADC=30°,BD=10,求⊙O的半径.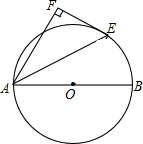 如图,AB是⊙0的直径,AE是弦,EF是⊙0的切线,E是切点,AF⊥EF,垂足为F,AE平分∠FAB吗?为什么?
如图,AB是⊙0的直径,AE是弦,EF是⊙0的切线,E是切点,AF⊥EF,垂足为F,AE平分∠FAB吗?为什么?