题目内容
2.小明在下面的计算中只做对了一道题,他做对的题目是( )| A. | ($\frac{a}{b}$)2=$\frac{{a}^{2}}{b}$ | B. | $\frac{1}{a}+\frac{1}{b}=\frac{2}{a+b}$ | C. | $\frac{{x}^{2}-{y}^{2}}{x-y}=x+y$ | D. | $\frac{-x-y}{x-y}=-1$ |
分析 根据分式混合运算的法则对各选项进行逐一判断即可.
解答 解:A、($\frac{a}{b}$)2=$\frac{{a}^{2}}{{b}^{2}}$≠$\frac{{a}^{2}}{b}$,故本选项错误;
B、$\frac{1}{a}$+$\frac{1}{b}$=$\frac{a+b}{ab}$≠$\frac{2}{a+b}$,故本选项错误;
C、$\frac{{x}^{2}-{y}^{2}}{x-y}$=$\frac{(x+y)(x-y)}{x-y}$=x+y,故本选项正确;
D、$\frac{-x-y}{x-y}$=-$\frac{x+y}{x-y}$≠-1,故本选项错误.
故选C.
点评 本题考查的是分式的混合运算,分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的.

练习册系列答案
相关题目
10.小明尝试着将矩形纸片ABCD(如图①,AD>CD)沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图②);再沿过D点的直线折叠,使得C点落在DA边上的点N处,E点落在AE边上的点M处,折痕为DG(如图③).如果第二次折叠后,M点正好在∠NDG的平分线上,那么矩形ABCD的长BC与宽AB的关系是( )
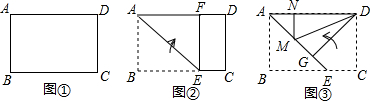

| A. | BC=2AB | B. | BC=$\sqrt{3}$AB | C. | BC=1.5AB | D. | BC=$\sqrt{2}$AB |
 、2、
、2、 D. 5、12、13
D. 5、12、13
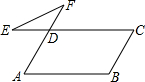 如图,在?ABCD中,∠B=120°,延长CD至点E,延长AD至点F,连结EF,则∠E+∠F=60度.
如图,在?ABCD中,∠B=120°,延长CD至点E,延长AD至点F,连结EF,则∠E+∠F=60度.