题目内容
 如图,抛物线与x轴交于B、C两点(点B在点C的右侧),其顶点为点A(1,4),且抛物线经过点B(4,0).
如图,抛物线与x轴交于B、C两点(点B在点C的右侧),其顶点为点A(1,4),且抛物线经过点B(4,0).(1)求点C的坐标及抛物线的解析式;
(2)动点P、Q分别从点C、B两点同时出发,均以每秒1个单位长度的速度分别沿CB、BA向终点B、A运动,问t为何值时,△PBQ是直角三角形;
(3)在y轴是否存在点M,使得△ABM是等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)根据抛物线的对称性可求出点C的坐标,因为知道抛物线的顶点坐标,所以可设设解析式为y=a(x-1)2+4,把B的坐标代入求出a的值即可;
(2)设对称轴x=1与x轴的交点为E,再分当Rt△PBQ∽Rt△ABE时,当Rt△PBQ∽Rt△EBA时,分别讨论,求出t的值即可;
(3)在y轴存在点M,使得△ABM是等腰三角形,易求AB的长,设M坐标为(0,m),分三种情况进行讨论,①当MB=MA时,②当MB=BA时,③当MA=AB时,分别求出满足△ABM是等腰三角形时m的值.
(2)设对称轴x=1与x轴的交点为E,再分当Rt△PBQ∽Rt△ABE时,当Rt△PBQ∽Rt△EBA时,分别讨论,求出t的值即可;
(3)在y轴存在点M,使得△ABM是等腰三角形,易求AB的长,设M坐标为(0,m),分三种情况进行讨论,①当MB=MA时,②当MB=BA时,③当MA=AB时,分别求出满足△ABM是等腰三角形时m的值.
解答:解:(1)∵抛物线顶点为点A(1,4),且抛物线经过点B(4,0).由点B和C关于x=1对称,
∴C(-2,0),
设解析式为y=a(x-1)2+4且过点B(4,0),
∴a=-
,
∴y=-
(x-1)2+4,
(2)PB=6-t,BQ=t,设对称轴x=1与x轴的交点为E,
①如图1,当Rt△PBQ∽Rt△ABE时,

∵A(1,4),B(4,0).
∴AB=
=
=5
∴
=
,
即有
=
∴t=
;
②如图2,当Rt△PBQ∽Rt△EBA时,

∵A(1,4),B(4,0).
∴BE=3,AB=
=
=5,
∴
=
,即有
=
∴t=
.
∴当t=
或t=
时,Rt△PBQ是直角三角形.
(3)在y轴存在点M,使得△ABM是等腰三角形,理由如下:
∵点A(1,4),点B(4,0),
∴AB=
=5,
①当MB=MA时,则AB为底,所以以作AB的垂直平分线交y轴,于M,此时M的坐标为(0,
);
②当MB=BA时,以B为圆心,BA长为半径画圆,和y轴有两个交点,交点坐标为(0,3)、(0,-3);
③当MA=AB时,以A为圆心,BA长为半径画圆,和y轴有两个交点,交点坐标为(0,4+2
)、(0,4-2
);
∴P点的坐标是(0,3)或(0,-3)或(0,4+2
)或(0,4-2
)或(0,
).
∴C(-2,0),
设解析式为y=a(x-1)2+4且过点B(4,0),
∴a=-
| 4 |
| 9 |
∴y=-
| 4 |
| 9 |
(2)PB=6-t,BQ=t,设对称轴x=1与x轴的交点为E,
①如图1,当Rt△PBQ∽Rt△ABE时,

∵A(1,4),B(4,0).
∴AB=
| AE2+BE2 |
| 42+(4-1)2 |
∴
| PB |
| AB |
| BQ |
| BE |
即有
| 6-t |
| 5 |
| t |
| 3 |
∴t=
| 9 |
| 4 |
②如图2,当Rt△PBQ∽Rt△EBA时,

∵A(1,4),B(4,0).
∴BE=3,AB=
| AE2+BE2 |
| 42+(4-1)2 |
∴
| PB |
| EB |
| BQ |
| BA |
| 6-t |
| 3 |
| t |
| 5 |
∴t=
| 15 |
| 4 |
∴当t=
| 9 |
| 4 |
| 15 |
| 4 |
(3)在y轴存在点M,使得△ABM是等腰三角形,理由如下:
∵点A(1,4),点B(4,0),
∴AB=
| AE2+BE2 |
①当MB=MA时,则AB为底,所以以作AB的垂直平分线交y轴,于M,此时M的坐标为(0,
| 1 |
| 8 |
②当MB=BA时,以B为圆心,BA长为半径画圆,和y轴有两个交点,交点坐标为(0,3)、(0,-3);
③当MA=AB时,以A为圆心,BA长为半径画圆,和y轴有两个交点,交点坐标为(0,4+2
| 6 |
| 6 |
∴P点的坐标是(0,3)或(0,-3)或(0,4+2
| 6 |
| 6 |
| 1 |
| 8 |
点评:本题主要考查二次函数的综合题,解答本题的关键是正确求出函数的解析式,解答第三问的时候需要分三种情况进行讨论,同学们很容易出现漏解的情况,请同学们解答的时候稍加注意.

练习册系列答案
相关题目
分式方程
=
的解为( )
| 3 |
| 2x |
| 1 |
| x-1 |
| A、x=4 | B、x=3 |
| C、x=2 | D、x=1 |
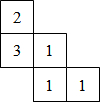 一个几何体由几块大小相同的小立方体达成,从上面观察这个几何体,看到的形状如图,其中小正方形中的数字表示在该位置小立方块的个数,请在下面相应的位置上画出这个几何体从正面、左面观察的形状图.
一个几何体由几块大小相同的小立方体达成,从上面观察这个几何体,看到的形状如图,其中小正方形中的数字表示在该位置小立方块的个数,请在下面相应的位置上画出这个几何体从正面、左面观察的形状图.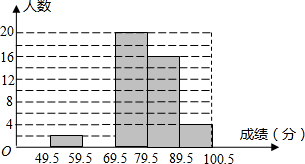 某校数学兴趣小组成员小华对本班上学期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析,绘制成频数分布直方图和频数、频率分布表.请你根据图表提供的信息,解答下列问题:
某校数学兴趣小组成员小华对本班上学期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析,绘制成频数分布直方图和频数、频率分布表.请你根据图表提供的信息,解答下列问题: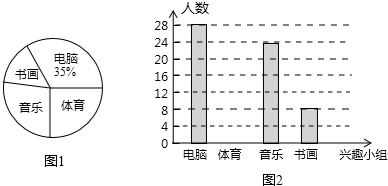
 如图,在?ABCD中,AC、BD相交于点O,AB⊥AC,AB=AC=2,求BD的长.
如图,在?ABCD中,AC、BD相交于点O,AB⊥AC,AB=AC=2,求BD的长. 已知△A′B′C′是由△ABC向上平移2个单位长度,再向右平移4个单位长度得到的,已知△ABC各顶点在平面直角坐标系中的坐标为:A(-1,0),B(3,-1),C(5,4).
已知△A′B′C′是由△ABC向上平移2个单位长度,再向右平移4个单位长度得到的,已知△ABC各顶点在平面直角坐标系中的坐标为:A(-1,0),B(3,-1),C(5,4). 如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AB=8,点E在AB边上,且CE平分∠BCD,DE平分∠ADC,则点E到CD的距离为
如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AB=8,点E在AB边上,且CE平分∠BCD,DE平分∠ADC,则点E到CD的距离为