Question

18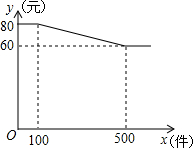．某服装厂A装，其单价y（元）与批发数量x（件）（x为正整数）之间的函
数关系如图所示．
（1）根据图象信息直接写出各段y与x的函数关系式．
（2）若批发商一次购进200件A装，所花钱数为多少？（其余费用不计）
（3）若每件A装成本为45元，当100＜x≤500件时（x为正整数），求服装厂所获利润w（元）与x之间的函数关系式，并求一次批发多少件时所获利润最大，最大利润为多少？

Answer 1

分析 （1）认真观察图象，分别写出该定义域下的函数关系式，定义域取值全部是整数；
（2）由（1）的函数解析式，把x值代入函数解析式，求出函数值；
（3）根据利润=（售价-成本）×件数，列出利润的表达式，求出最值．

解答 解：（1）当0＜x≤100且x为整数（或x取1，2，3，100）时，y=80；
当100＜x≤500且x为整数（或x取101，102，500）时，y=-$\frac{1}{20}$x+85；
当x＞500且x为整数（或x取501，502，503）时，y=60．
（2）当x=200时，y=-$\frac{1}{20}$×200+85=75，
∴所花的钱数为75×200=15000（元）．
（3）当100＜x≤500且x为整数时，y=-$\frac{1}{20}$x+85，
∴w=（y-45）x=（-$\frac{1}{20}$x+85-45）x，
∴w=-$\frac{1}{20}$x²+40x，
∴w=-$\frac{1}{20}$（x-400）²+8000，
∵-$\frac{1}{20}$＜0，
∴当x=400时，w最大，最大值为8000元．
答：一次批发400件时所获利润最大，最大利润是8000元．

点评 本题主要考查一次函数和二次函数的应用，根据题意列出函数表达式并熟练运用性质是解决问题的关键．